【题目】在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算?
参考答案:
【答案】
(1)解:设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,
y=30x+90(100﹣x)=9000﹣60x
(2)解:设购买A种树苗x棵,则B种树苗(100﹣x)棵,根据题意得:
![]() ,
,
解得:24≤x≤25,
因为x是正整数,
所以x只能取25,24.
有两种购买树苗的方案:
方案一:购买A种树苗25棵时,B种树苗75棵;
方案二:购买A种树苗24棵时,B种树苗76棵
(3)解:∵y=9000﹣60x,﹣60<0,
∴y随x的增大而减小,
又x=25或24,
∴采用购买A种树苗25棵,B种树苗75棵时更合算
【解析】(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,根据某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元可列出函数关系式.(2)根据购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵树不少于A种树苗棵树的3倍,列出不等式组,解不等式组即可得出答案;(3)根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
【考点精析】通过灵活运用一元一次不等式组的应用,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题:
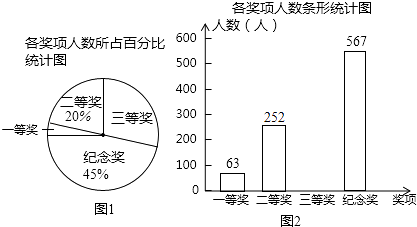
(1)该校共有名学生;
(2)在图①中,“三等奖”所对应扇形的圆心角度数是;
(3)将图②补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B.
 C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.

(1)求证:DF=AE;
(2)当AB=2时,求BE2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场促销,小鱼将促销信息告诉了妈妈,假设某一商品的定价为
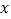 ,并列出不等式为
,并列出不等式为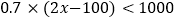 ,那么小鱼告诉妈妈的信息是( )
,那么小鱼告诉妈妈的信息是( )A. 买两件等值的商品可减100元,再打三折,最后不到1000元
B. 买两件等值的商品可打三折,再减100元,最后不到1000元
C. 买两件等值的商品可减100元,再打七折,最后不到1000元
D. 买两件等值的商品可打七折,再减100元,最后不到1000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线,作过C点且与AC垂直的直线,交于P点,则P即为所求.
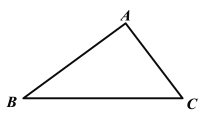
对于甲、乙两人的作法,下列叙述何者正确?( )
A. 两人皆正确
B. 两人皆错误
C. 甲正确,乙错误
D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D.
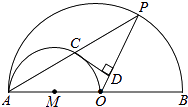
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
相关试题

