【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
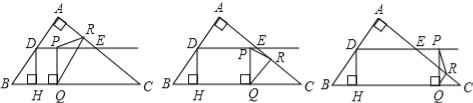
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)y=-
(2)y=-![]() x+6(3)存在,
x+6(3)存在,![]() 或6或
或6或![]()
【解析】
试题分析:(1)根据三角形相似的判定定理求出△BHD∽△BAC,根据相似三角形的性质求出DH的长;
(2)根据△RQC∽△ABC,根据三角形的相似比求出y关于x的函数关系式;
(3)画出图形,根据图形进行讨论:
①当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,∴∠1=∠C.
∴cos∠1=cosC=![]() ,∴
,∴![]() ,即可求出x的值;
,即可求出x的值;
②当PQ=RQ时,﹣![]() x+6=
x+6=![]() ,x=6;
,x=6;
③当PR=QR时,则R为PQ中垂线上的点,于是点R为EC的中点,故CR=![]() CE=
CE=![]() AC=2.由于tanC=
AC=2.由于tanC=![]() ,x=
,x=![]() .
.
试题解析:(1)在Rt△ABC中,
∵∠A=90°,AB=6,AC=8,
∴BC=![]() =10.
=10.
∵∠DHB=∠A=90°,∠B=∠B.
∴△BHD∽△BAC,
∴![]() ,
,
∴DH=![]() AC=
AC=![]() ×8=
×8=![]()
(2)∵QR∥AB,
∴∠QRC=∠A=90°.
∵∠C=∠C,
∴△RQC∽△ABC,
∴![]() ,∴
,∴![]() ,
,
即y关于x的函数关系式为:y=-![]() x+6.
x+6.
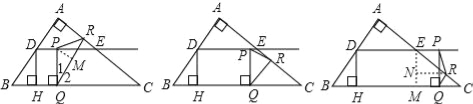
(3)存在,分三种情况:
①当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.
∵∠1+∠2=90°,∠C+∠2=90°,
∴∠1=∠C.
∴cos∠1=cosC=![]() ,
,
∴![]() ,
,
∴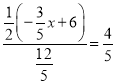 ,
,
∴x=![]() .
.
②当PQ=RQ时,﹣![]() x+6=
x+6=![]() ,
,
∴x=6.
③作EM⊥BC,RN⊥EM,
∴EM∥PQ,
当PR=QR时,则R为PQ中垂线上的点,
∴EN=MN,
∴ER=RC,
∴点R为EC的中点,
∴CR=![]() CE=
CE=![]() AC=2.
AC=2.
∵tanC=![]() ,
,
∴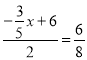 ,
,
∴x=![]() .
.
综上所述,当x为![]() 或6或
或6或![]() 时,△PQR为等腰三角形.
时,△PQR为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接对角线相等的四边形的各边中点,所得图形一定是( )
A. 平行四边形B. 矩形C. 菱形D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决群众看病难的问题,一种药品连续两次降价,每盒的价格由原来的60元降至48.6元,则平均每次降价的百分率为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ACD是△ABC分别以AB、AC为对称轴翻折180°形成的,若∠1︰∠2︰∠3=28︰5︰3,则∠α度数为______________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
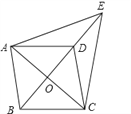
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大型记录电影《厉害了,我的国》3月2日在全国上映,在上映首日收获了4132万人民币的票房,数据“4132万”用科学记数法表示为( )
A. 41.32×106 B. 4.132×107 C. 4.132×106 D. 41.32×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的周长为81cm,三边长的比为2:3:4,则最长边比最短边长cm.
相关试题

