【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
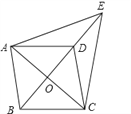
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
参考答案:
【答案】(1)四边形ABCD是菱形,理由见解析;(2)理由见解析.
【解析】分析:(1)根据对角线互相垂直的平行四边形是菱形.∵△ACE是等边三角形,∴EO⊥AC(三线合一),即AC⊥BD.∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠DAO=∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠DAB=2∠ADO=90°,∴四边形ABCD是正方形.
解:(1)四边形ABCD是菱形,理由如下:
∵四边形ABCD是平行四边形 ∴OA=OC,即O是AC的中点.
∵△ACE是等边三角形. ∴OE⊥AC, ∴BD⊥AC, ∴□ABCD是菱形;
(2)∵四边形ABCD是平行四边形, ∴AO=CO
∵△ACE是等边三角形 ∴∠AEC=∠EAC=60°,∠AED=30°,
∵∠AED=2∠EAD, ∴∠EAD=15° ∴∠DAO=∠ADO=45°,
∵四边形ABCD是菱形; ∴∠DAB=90° ∴四边形ABCD是正方形.
点睛: 此题主要考查菱形和正方形的判定,要灵活应用判定定理及等腰三角形的性质、外角的性质定理:对角线互相垂直的平行四边形是菱形;有一个角是直角的菱形是正方形;三角形的一个外角等于和它不相邻的两内角之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决群众看病难的问题,一种药品连续两次降价,每盒的价格由原来的60元降至48.6元,则平均每次降价的百分率为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ACD是△ABC分别以AB、AC为对称轴翻折180°形成的,若∠1︰∠2︰∠3=28︰5︰3,则∠α度数为______________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
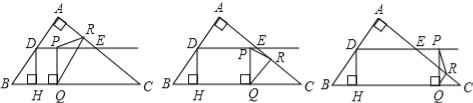
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大型记录电影《厉害了,我的国》3月2日在全国上映,在上映首日收获了4132万人民币的票房,数据“4132万”用科学记数法表示为( )
A. 41.32×106 B. 4.132×107 C. 4.132×106 D. 41.32×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的周长为81cm,三边长的比为2:3:4,则最长边比最短边长cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.

相关试题

