【题目】计算
(1)(﹣2xy2)23x2y÷(﹣x3y4)
(2)(2x+y)(2x﹣3)﹣2y(x﹣1)
(3)3(m+1)2﹣5(m+1)(m﹣1)+2(m﹣1)2
(4)![]()
参考答案:
【答案】(1)﹣12xy;(2)4x2﹣6x﹣y;(3)2m+10;(4)﹣4x+2x2y+y2
【解析】
(1)根据单项式乘单项式的法则,单项式除单项式的法则化简即可;
(2)根据多项式乘多项式的法则,合并同类项的法则化简即可;
(3)根据完全平方公式,多项式乘多项式的法则,合并同类项的法则化简即可;
(4)根据多项式除单项式的法则去括号化简即可
解:(1)原式=﹣22x2y43x2y÷x3y4
=﹣12x4y5÷x3y4
=﹣12xy
(2)原式=4x2﹣6x+2xy﹣3y﹣2xy+2y
=4x2﹣6x﹣y
(3)原式=3(m2+2m+1)﹣5(m2﹣1)+2(m2﹣2m+1)
=3m2+6m+3﹣5m2+5+2m2﹣4m+2
=2m+10
(4)原式=﹣(2x2y﹣x3y2﹣![]() xy3)×2x﹣1y﹣1
xy3)×2x﹣1y﹣1
=﹣2x2y×2x﹣1y﹣1+x3y2×2x﹣1y﹣1+![]() xy3×2x﹣1y﹣1
xy3×2x﹣1y﹣1
=﹣4x+2x2y+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为地铁调价后的计价表.调价后小明、小伟从家到学校乘地铁分别需要4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校的里程多5 km,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m
0<m≤100
100<m≤200
m>200
收费标准(元/人)
90
85
75
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
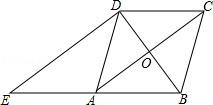
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划从一厂家购进若干部新型手机以满足市场需求.已知该厂家生产三种不同型号的手机,出厂价分别是甲种型号手机1800元/部,乙种型号手机600元/部,丙种型号手机1200元/部.商场在经销中,甲种型号手机可赚200元/部,乙种型号手机可赚100元/部,丙种型号手机可赚120元/部.
(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案.
相关试题

