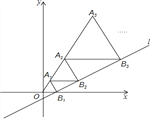
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A100的横坐标是_____.
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A100的横坐标是_____.
参考答案:
【答案】![]()
【解析】分析: 先根据直线l:y=![]() x-
x-![]() 与x轴交于点B1,可得B1(1,0),OB1=1,∠OB1D=30°,再过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为
与x轴交于点B1,可得B1(1,0),OB1=1,∠OB1D=30°,再过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为![]() ,A2的横坐标为
,A2的横坐标为![]() ,A3的横坐标为
,A3的横坐标为![]() ,进而得到An的横坐标为
,进而得到An的横坐标为![]() ,据此可得点A100的横坐标.
,据此可得点A100的横坐标.
详解: 由直线l:y=![]() x-
x-![]() 与x轴交于点B1,可得B1(1,0),D(0,-
与x轴交于点B1,可得B1(1,0),D(0,-![]() ),
),
∴OB1=1,∠OB1D=30°,
如图所示,过A1作A1A⊥OB1于A,则OA=![]() OB1=
OB1=![]() ,
,
即A1的横坐标为![]() =
=![]() ,
,
由题可得∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,
∴∠A1B1B2=90°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=![]() A1B2=1,
A1B2=1,
即A2的横坐标为![]() +1=
+1=![]() =
=![]() ,
,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=![]() A2B3=2,
A2B3=2,
即A3的横坐标为![]() +1+2=
+1+2=![]() =
=![]() ,
,
同理可得,A4的横坐标为![]() +1+2+4=
+1+2+4=![]() =
=![]() ,
,
由此可得,An的横坐标为![]() ,
,
∴点A2018的横坐标是![]() ,
,
故答案为:![]() .
.
点睛: 本题主要考查了一次函数图象上点的坐标特征以及等边三角形的性质的运用,解决问题的关键是依据等边三角形的性质找出规律,求得An的横坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.

-
科目: 来源: 题型:
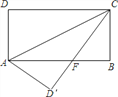
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,则重叠部分S△AFC=_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
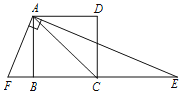
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(
 ,1)在射线OM上,点B(
,1)在射线OM上,点B( ,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2,
,3)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,以A1B1为直角边作第三个Rt△A1B1A2, ,依此规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为__.
,依此规律,得到Rt△B2017A2018B2018,则点B2018的纵坐标为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对市区居民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
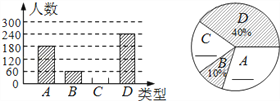
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?并将两幅不完整的图补充完整;
(2)若常德市武陵区居民有60万人口,估计有多少人爱吃肉馅粽?
(3)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
相关试题

