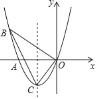
【题目】如图,已知抛物线y=ax2+bx经过点A(﹣2,0)、B(﹣3,3),顶点为C.
(1)求抛物线的函数表达式;
(2)若点P是第一象限内的抛物线上一动点,过点P作PM⊥x轴于点M,则是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) y=x2+2x;(2)见解析.
【解析】
(1)利用待定系数法直接求出抛物线的解析式;(2)分两种情况讨论,①若△AMP∽△BOC,②若△PMA∽△BOC,根据相似三角形对应边的比相等可以求出P点坐标.
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),且过A(﹣2,0),B(﹣3,3),O(0,0)可得
![]() ,
,
解得:![]() .
.
故抛物线的解析式为:y=x2+2x;
(2)存在,
如图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2.
∴△BOC是直角三角形.
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
①若△AMP∽△BOC,则![]() =
=![]() ,
,
即 x+2=3(x2+2x)
得:x1=![]() ,x2=﹣2(舍去).
,x2=﹣2(舍去).
当x=![]() 时,y=
时,y=![]() ,即P(
,即P(![]() ,
,![]() ).
).
②若△PMA∽△BOC,则![]() =
=![]() ,
,
即:x2+2x=3(x+2)
得:x1=3,x2=﹣2(舍去)
当x=3时,y=15,即P(3,15).
故符合条件的点P有两个,分别是P(![]() ,
,![]() )和(3,15).
)和(3,15).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知等腰直角
 中,BD为斜边上的中线,E为DC上的一点,且
中,BD为斜边上的中线,E为DC上的一点,且 于G,AG交BD于F.
于G,AG交BD于F.(1)求证:AF=BE.
(2)如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是
 ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是
 ,底相等的两个等腰三角形
,底相等的两个等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有( )①图1中的BC长是8cm,②图2中的M点表示第4秒时y的值为24cm2,③图1中的CD长是4cm,④图2中的N点表示第12秒时y的值为18cm2,⑤图1的总面积为72 cm2

A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(-2,-3),B(1,0),C(3,4),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图
 ,已知
,已知 是⊙
是⊙ 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点 ,使
,使 为“智慧三角形”(画出点
为“智慧三角形”(画出点 的位置,保留作图痕迹);
的位置,保留作图痕迹);⑵如图
 ,在正方形
,在正方形 中,
中, 是
是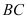 的中点,
的中点, 是
是 上一点,且
上一点,且 ,试判断
,试判断 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;运用:
⑶如图
 ,在平面直角坐标系
,在平面直角坐标系 中,⊙
中,⊙ 的半径为
的半径为 ,点
,点 是直线
是直线 上的一点,若在⊙
上的一点,若在⊙ 上存在一点
上存在一点 ,使得
,使得 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点 的坐标.
的坐标.
相关试题

