【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(![]() ≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是
≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是![]() ,平均销售价格为9万元/吨.
,平均销售价格为9万元/吨.
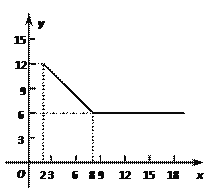
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入-经营总成本)
(3)若该公司收购20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元.
①求w关于x的函数关系式;
②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?
参考答案:
【答案】(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨9万元;(2)此时经营这批杨梅所获得的毛利润w为30万元;(3)当毛利润达到30万元时,用于直销的A类杨梅为18吨.
【解析】试题分析:(1)用待定系数法求得y与x的函数解析式,把x=5代入即可;
(2)根据“毛利润=销售总收入﹣经营总成本”计算即可求得结论;
(3)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=wA+wB﹣3×20;
②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量.
试题解析:解:(1)设x,y的解析式为y=kx+b,把x=2时,y=12,x=8时,y=6得: ![]()
解得: ![]() ,∴y=﹣x+14(2≤x≤8),∴x=5时,y=9.
,∴y=﹣x+14(2≤x≤8),∴x=5时,y=9.
答:A类杨梅的销售量为5吨时,它的平均销售价格是每吨9万元;
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则B类杨梅有6吨,易得:WA=(10﹣3﹣1)×4=24(万元),WA=6×(9﹣3)﹣(12+3×6)=6(万元),∴W=24+6=30(万元).
答:此时经营这批杨梅所获得的毛利润w为30万元;
(3)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨,①当2≤x<8时,wA=x(﹣x+14)﹣x=﹣x2+13x,wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x,∴w=wA+wB﹣3×20
=(﹣x2+13x)+(108﹣6x)﹣60
=﹣x2+7x+48;
当x≥8时,wA=6x﹣x=5x,wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x
∴w=wA+wB﹣3×20
=(5x)+(108﹣6x)﹣60
=﹣x+48,∴w关于x的函数关系式为:
w=![]() ;
;
②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意.
当x≥8时,﹣x+48=30,解得x=18,∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张正方形纸片,第1次剪成四个大小形状一样的小正方形,第2次将其中的一个小正方形再按同样的方法剪成四个小正方形,然后再将其中的一个小正方形剪成四个小正方形,如此循环进行下去,如果共剪
 次,则可剪出 个正方形.
次,则可剪出 个正方形.
-
科目: 来源: 题型:
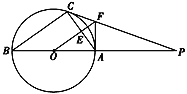
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连结AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若AC=24,AF=15,求sinB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点A,B,C 在数轴上,对应表示的数是a,b,c.
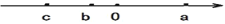
(1)填空:A、B 之间的距离为 ;B、C 之间的距离为 ;A、C 之间的距离为 ;
(2)化简:|a+b|-|c-b|-|b-a|+|c|
(3)若 c2=9,-b 的倒数是它本身,a 的绝对值是 2,求(2a+b)-(c-b)-(a+2b-3c)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月世界计算机大会在湖南省长沙市开幕,大会的主题是“计算万物,湘约未来”.从心算、珠算的古老智慧到“银河”“天河”“神威”创造的中国速度,“中国计算”为世界瞩目.超级计算机“天河一号”的性能是4700万亿次,换算成人工做四则运算,相当于60亿人算一年,它1秒就可以完成.数4700万亿用科学记数法表示为( )

A.
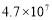 B.
B.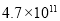 C.
C. D.
D.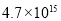
-
科目: 来源: 题型:
查看答案和解析>>【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
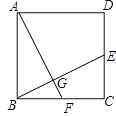
A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
相关试题

