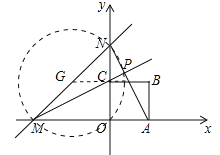
【题目】如图直线y=x+2分别与x轴,y轴交于点M、N,边长为1的正方形OABC的一个顶点O在坐标系原点,直线AN与MC交于点P,若正方形绕点O旋转一周,则点P到点(0,1)长度的最小值是___________.

参考答案:
【答案】![]()
【解析】解:在△MOC和△NOA中,∵OA=OC,∠MOC=∠AON,OM=ON,∴△MOC≌△NOA,∴∠CMO=∠ANO.∵∠CMO+∠MCO=90°,∠MCO=∠NCP,∴∠NCP+∠CNP=90°,∴∠MPN=90°,∴MP⊥NP.在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,∴P在以MN为直径的圆上.∵M(﹣2,0),N(0,2),∴圆心G为(﹣1,1),半径为![]() .∵PG﹣GC≤PC,∴当圆心G,点P,C(0,1)三点共线时,PC最小.∵GN=GM,CN=CO=1,∴GC=
.∵PG﹣GC≤PC,∴当圆心G,点P,C(0,1)三点共线时,PC最小.∵GN=GM,CN=CO=1,∴GC=![]() OM=1,这个最小值为GP﹣GC=
OM=1,这个最小值为GP﹣GC=![]() .故答案为:
.故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;

(2)填表:
平均数(分)
中位数(分)
众数(分)
一班
a
b
85
二班
84
75
c
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.
-
科目: 来源: 题型:
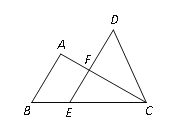
查看答案和解析>>【题目】如图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=2,AB=3,则DF的长等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为
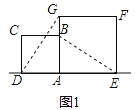
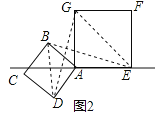
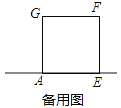
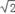 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,A为x轴正半轴上的动点,经过点A(t,0)作垂直于x轴的直线l,在直线l上取点B,点B在第一象限,AB=4,直线OB:y1=kx(k为常数).
(1)当t=2时,求k的值;
(2)经过O,A两点作抛物线y2=ax(x﹣t)(a为常数,a>0),直线OB与抛物线的另一个交点为C.
①用含a,t的式子表示点C的横坐标;
②当t≤x≤t+4时,|y1﹣y2|的值随x的增大而减小;当x≥t+4时,|y1﹣y2|的值随x的增大而增大,求a与t的关系式并直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=
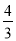 ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.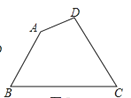
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )
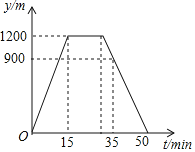
A. 小涛家离报亭的距离是900m
B. 小涛从家去报亭的平均速度是60m/min
C. 小涛从报亭返回家中的平均速度是80m/min
D. 小涛在报亭看报用了15min
相关试题

