【题目】在平面直角坐标系中,O为原点,A为x轴正半轴上的动点,经过点A(t,0)作垂直于x轴的直线l,在直线l上取点B,点B在第一象限,AB=4,直线OB:y1=kx(k为常数).
(1)当t=2时,求k的值;
(2)经过O,A两点作抛物线y2=ax(x﹣t)(a为常数,a>0),直线OB与抛物线的另一个交点为C.
①用含a,t的式子表示点C的横坐标;
②当t≤x≤t+4时,|y1﹣y2|的值随x的增大而减小;当x≥t+4时,|y1﹣y2|的值随x的增大而增大,求a与t的关系式并直接写出t的取值范围.
参考答案:
【答案】(1)k=2;(2)当t≤x≤t+4时,|y1﹣y2|的值随x的增大而减小;当x≥t+4时,|y1﹣y2|的值随x的增大而增大时,a与t的关系式a=![]() (t≥4).
(t≥4).
【解析】分析:(1)找出当t=2时,B点的坐标,将其代入直线OB:y1=kx中即可;
(2)①用t表示出直线OB的关系式,令y1=y2,即可用含a,t的式子表示点C的横坐标;
②找出![]() 的关系式,发现为一个开口向下的抛物线,结合给定条件能够得知,抛物线的对称轴不超过
的关系式,发现为一个开口向下的抛物线,结合给定条件能够得知,抛物线的对称轴不超过![]() ,且抛物线与x轴的另一个交点为(t+4,0).由此可得出a与t的关系式并能知道t的取值范围.
,且抛物线与x轴的另一个交点为(t+4,0).由此可得出a与t的关系式并能知道t的取值范围.
详解:(1)当t=2时,点A的坐标为(2,0),
∵经过点A(t,0)作垂直于x轴的直线l,在直线l上取点B,点B在第一象限,AB=4,
∴点B的坐标为(2,4).
∵点B在直线OB:y1=kx(k为常数)上,
∴有4=2k,解得:k=2.
(2)①点B(t,4)在直线OB:y1=kx上,
∴有4=kt,解得:![]()
∴![]()
令y1=y2,即![]()
解得:x=0或者![]()
故点C的横坐标![]()
②![]()
∵a>0,
∴a<0,函数图象开口向下,函数图象大体如下图:
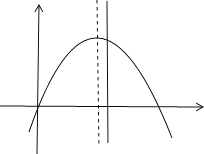
∵当![]() 时,
时,![]() 的值随x的增大而减小;当
的值随x的增大而减小;当![]() 时,
时, ![]() 的值随x的增大而增大,
的值随x的增大而增大,
∴二次函数![]() 的对称轴在x=t的左侧或者重合,而且二次函数
的对称轴在x=t的左侧或者重合,而且二次函数![]() 与x轴的另一个交点为(t+4,0).
与x轴的另一个交点为(t+4,0).
∵![]()
∴有![]()
解得:![]()
二次函数对称轴![]() 即
即![]()
∵at=1,
∴![]()
故当![]() 时,
时,![]() 的值随x的增大而减小;当
的值随x的增大而减小;当![]() 时,
时, ![]() 的值随x的增大而增大时,a与t的关系式
的值随x的增大而增大时,a与t的关系式![]() (
(![]() ).
).
-
科目: 来源: 题型:
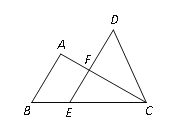
查看答案和解析>>【题目】如图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=2,AB=3,则DF的长等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为
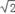 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.(1)图1中,小明发现DG=BE,请你帮他说明理由.
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.
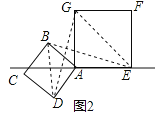
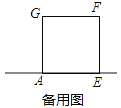
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图直线y=x+2分别与x轴,y轴交于点M、N,边长为1的正方形OABC的一个顶点O在坐标系原点,直线AN与MC交于点P,若正方形绕点O旋转一周,则点P到点(0,1)长度的最小值是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=
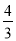 ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )
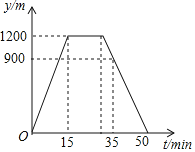
A. 小涛家离报亭的距离是900m
B. 小涛从家去报亭的平均速度是60m/min
C. 小涛从报亭返回家中的平均速度是80m/min
D. 小涛在报亭看报用了15min
-
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上直接写出下列算式的运算结果.
(1)(+3)+(-8)=__________________.
(2)0-(-6)=__________________.
(3)
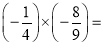 _____________________.
_____________________.(4)
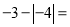 __________________.
__________________.(5)
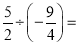 _____________________.
_____________________.(6)
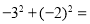 __________________.
__________________.
相关试题

