【题目】如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
(1)用关于x的代数式表示PA+PD;
(2)求出PA+PD的最小值;
(3)仿(2)的做法,构造图形,求![]() 的最小值;
的最小值;
(4)直接写出![]() 的最小值.
的最小值.

参考答案:
【答案】(1)![]() ;(2)10,(3)
;(2)10,(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据勾股定理可直接用x表示PA+PD即可;
(2)作A关于BC的对称点E,连接DE,根据轴对称确定最短路线问题,则DE就是PA+PD的最小值,然后利用勾股定理列式计算即可得解;
(3)设DC=1,AB=3,BC=6,根据(2)结论;即可得到结果;
(4)设DC=2,AB=3,BC=5,PC=2+x,则BP=3-x,根据(2)结论即可得到结果.
(1)∵AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,
∴PA+PD=![]()
![]() ,
,
![]() ;
;
(2)作A关于BC的对称点E,连接DE,则DE就是PA+PD的最小值,BE=AB=4,
过E作EF∥BC交DC的延长线于F,则四边形BEFC是矩形,
∴EF=BC=8,DF=2+4=6,
∴DE=![]() =10,
=10,
∴PA+PD的最小值是10;

(3)设DC=1,AB=3,BC=6,则EF=6,DF=3+1=4,
∴DE=![]() =2
=2![]() ,
,
∴![]() 的最小值是2
的最小值是2![]() ;
;
(4)设DC=2,AB=3,BC=5,PC=2+x,则BP=3-x,EF=5,DF=3+2=5,
∴DE=![]() =5
=5![]() ,
,
∴![]() 的最小值是5
的最小值是5![]() .
.
-
科目: 来源: 题型:
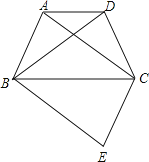
查看答案和解析>>【题目】如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
-
科目: 来源: 题型:
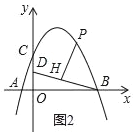
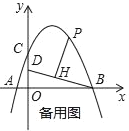
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=
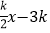 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.(1)求抛物线的解析式;
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=
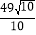 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.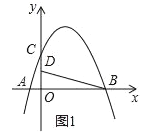
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式,并探究
①

②

③

……
(1)写出第④个等式:______;
(2)某同学发现,四个连续自然数的积加上1后,结果都将是某一个整数的平方.当这四个数较大时可以进行简便计算,如:
 .
.请你猜想写出第n个等式,用含有n的代数式表示,并通过计算验证你的猜想.
(3)任何实数的平方都是非负数(即
 ),一个非负数与一个正数的和必定是一个正数(即
),一个非负数与一个正数的和必定是一个正数(即 时,
时, ).根据以上的规律和方法试说明:无论x为什么实数,多项式
).根据以上的规律和方法试说明:无论x为什么实数,多项式 的值永远都是正数.
的值永远都是正数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于A,B两点,且点B坐标为(3,0).
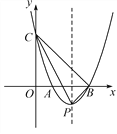
(1)求抛物线的表达式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
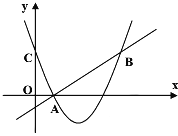
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.

相关试题

