【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.

(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论.
参考答案:
【答案】见解析;矩形.
【解析】试题分析:因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有AF=DC;由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
试题解析:(1)∵AF∥DC, ∴∠AFE=∠DCE, 又∵∠AEF=∠DEC(对顶角相等),AE=DE(E为AD的中点),
∴△AEF≌△DEC(AAS),∴AF=DC;
(2)矩形.
由(1),有AF=DC且AF∥DC, ∴四边形AFDC是平行四边形, 又∵AD=CF,
∴AFDC是矩形(对角线相等的平行四边形是矩形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能化简(x﹣1)(x99+x98+…+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手.然后归纳出一些方法.
(1)分别化简下列各式:
(x﹣1)(x+1)= ;
(x﹣1)(x2+x+1)= ;
(x﹣1)(x3+x2+x+1)= ;
…
(x﹣1)(x99+x98+…+x+1)= .
(2)请你利用上面的结论计算:
299+298+…+2+1
399+398+…+3+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D(D不与A、B重合),当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC.此时BE与DC有怎样的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
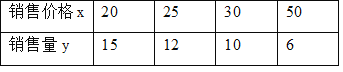
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式.
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列每个图形中(每个图形都各自独立),是否存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.

-
科目: 来源: 题型:
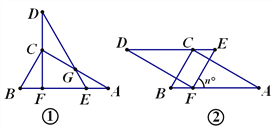
查看答案和解析>>【题目】已知△ABC、△DEF是两个完全一样的三角形,其中∠ACB=∠DFE=90°,∠A=∠D=30°.
(1)将它们摆成如图①的位置(点E、F在AB上,点C在DF上,DE与AC相交于点G).求∠AGD的度数.
(2)将图①的△ABC固定,把△DEF绕点F按逆时针方向旋转n°.
①当△DEF旋转到DE∥AB的位置时(如图2), n = ;
②若由图①旋转后的EF能与△ABC的一边垂直,则n的值为 .
相关试题

