【题目】已知△ABC、△DEF是两个完全一样的三角形,其中∠ACB=∠DFE=90°,∠A=∠D=30°.
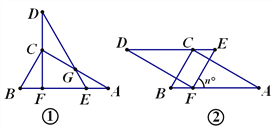
(1)将它们摆成如图①的位置(点E、F在AB上,点C在DF上,DE与AC相交于点G).求∠AGD的度数.
(2)将图①的△ABC固定,把△DEF绕点F按逆时针方向旋转n°.
①当△DEF旋转到DE∥AB的位置时(如图2), n = ;
②若由图①旋转后的EF能与△ABC的一边垂直,则n的值为 .
参考答案:
【答案】(1)150°;(2)①60,②60或90或150.
【解析】试题分析:(1)根据三角形内角和与外角的性质可得∠DEA=∠DFE+∠D,∠AGD=∠A+∠DEA;
(2)①根据平行线的性质可得∠EFA=∠E;
②此题要分情况讨论:当EF⊥AC时;当EF⊥AB时;当EF⊥BC时分别进行计算.
试题解析:(1)∵∠DFE=90°,∠D=30°,
∴∠DEA=30°+90°=120°,
∵∠A=30°,
∴∠DGA=120°+30°=150°;
(2)①∵∠DFE=90°,∠D=30°,
∴∠E=60°,
∵DE∥AB,
∴∠E=∠EFA=60°,
∴n=60,
故答案为:60;
②当EF⊥AC时,n=180-90-30=60,
当EF⊥AB时,n=90,
当EF⊥BC时,n=360-30-90-90=150,
故答案为:60或90或150.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.

(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
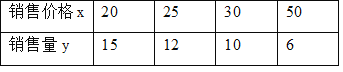
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式.
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列每个图形中(每个图形都各自独立),是否存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
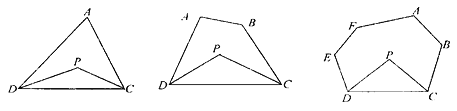
图1 图2 图3
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
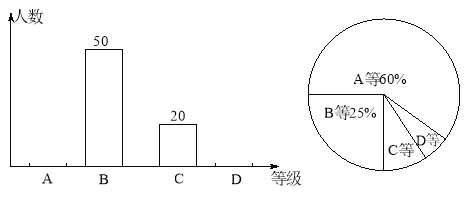
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
相关试题

