【题目】如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.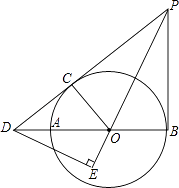
(1)求证:PB是⊙O的切线;
(2)若PB=9,DB=12,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线
(2)解:在Rt△PBD中,PB=9,DB=12,
根据勾股定理得:PD= ![]() =15,
=15,
∵PD与PB都为圆的切线,
∴PC=PB=9,
∴DC=PD﹣PC=15﹣9=6,
在Rt△CDO中,设OC=r,则有DO=12﹣r,
根据勾股定理得:(12﹣r)2=r2+62,
解得:r=4.5,
则圆的半径为4.5
【解析】(1)由已知在△DEO和△PBO中,∠EDB=∠EPB及对顶角相等,得出∠OBP=∠E,再根据垂直的定义证得∠OBP是直角,即可得证。
(2)先在Rt△PBD中根据勾股定理求出PD的长,再根据切线长定理得出PC=PB,再转化到Rt△CDO中根据勾股定理建立方程,即可求出圆的半径。
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
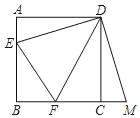
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF=MF;(2)当AE=1时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )

A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
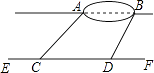
查看答案和解析>>【题目】小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明过程,并在括号内填上依据.
如图,点E在AB上,点F在CD上,∠1=∠2,∠B=∠C,求证AB∥CD.
证明:∵∠1=∠2(已知),∠1=∠4( ),
∴∠2= (等量代换),
∴ ∥BF( ),
∴∠3=∠ ( ).
又∵∠B=∠C(已知),
∴∠3=∠B( ),
∴AB∥CD( ).

-
科目: 来源: 题型:
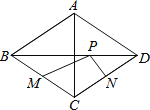
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 ____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
相关试题

