【题目】为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);
(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;
(3)如果从最高气温不低于24℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.
参考答案:
【答案】
(1)
这30天最高气温的平均数为: ![]() =20.4℃;
=20.4℃;
∵中位数落在第三组内,
∴中位数为22℃;
(2)
∵30天中,最高气温超过(1)中平均数的天数为16天,
∴该地这个季度中最高气温超过(1)中平均数的天数为 ![]() ×90=48(天)
×90=48(天)
(3)
从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,
故这两天都在气温最高一组内的概率为 ![]() =
= ![]()
【解析】(1)根据30天的最高气温总和除以总天数,即可得到这30天最高气温的平均数,再根据第15和16个数据的位置,判断中位数;(2)根据30天中,最高气温超过(1)中平均数的天数,即可估计这个季度中最高气温超过(1)中平均数的天数;(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,据此可得这两天都在气温最高一组内的概率.
【考点精析】解答此题的关键在于理解算术平均数的相关知识,掌握总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数,以及对中位数、众数的理解,了解中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|2﹣ |﹣
|﹣  (
(  ﹣
﹣  )+
)+  ;
;
(2)先化简,再求值: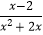 ÷
÷ 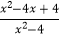 +
+ 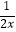 ,其中x=﹣
,其中x=﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.

(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某专卖店有A,B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
 >
>  x﹣1.
x﹣1.
(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)

相关试题

