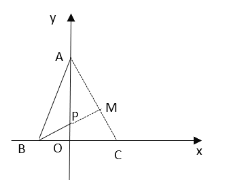
【题目】如图,在平面直角坐标系中,点 A 在 y 轴正半轴上点 B 在 x 轴负半轴上,且 AB=2,∠BAO=15°,点 P 是线段OA 上的一个动点,则 PB ![]() PA 的最小值为_____________.
PA 的最小值为_____________.

参考答案:
【答案】![]() .
.
【解析】
在y轴右侧取∠OAC=30°,过点P作PM⊥AC,利用含30°的直角三角形的性质求得PM=![]() ,然后利用两点之间线段最短分析得出当点B,P,M三点共线时PB PM最小,即BM的长,从而利用等腰直角三角形的性质求解.
,然后利用两点之间线段最短分析得出当点B,P,M三点共线时PB PM最小,即BM的长,从而利用等腰直角三角形的性质求解.
解:在y轴右侧取∠OAC=30°,过点P作PM⊥AC
∵在Rt△OAC中,∠OAC=30°
∴PM=![]()
∴PB ![]() PA= PB PM
PA= PB PM
∴当点B,P,M三点共线时PB PM最小,即BM的长
又∵∠BAO=15°,∠OAC=30°,PM⊥AC
∴在Rt△ABM中,∠BAM=45°
∴BM=![]()
则PB ![]() PA 的最小值为
PA 的最小值为![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,顺次连接长宽不等的矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边中点,得到图 3.如 此反复操作下去,则第 2021 个图形中直角三角形的个数有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
A.
B.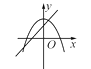
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD 中,点 E,F 分别在 AB,CD 上,且 AE=CF.

(1)求证:四边形 AECF 是平行四边形;
(2)直接写出 CE 与 AE 满足 时, AECF是矩形;
(3)直接写出 CE 与 AE 满足 时, AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(有阴影部分)面积之和为S2 , 则
 =( )
=( )
A.
B.
C.
D.1
相关试题

