【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
参考答案:
【答案】
(1)解:把A(3,0),B(2,﹣3),C(0,﹣3)代入y=ax2+bx+c得:
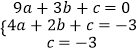 ,
,
解得: 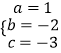 ,
,
则抛物线解析式为y=x2﹣2x﹣3
(2)解:把x=﹣2代入抛物线解析式得:y=5,即D(﹣2,5),
∵A(3,0),即OA=3,
∴S△AOD= ![]() ×3×5=
×3×5= ![]()
【解析】(1)把A,B,C三点坐标代入解析式求出a,b,c的值,即可求出函数解析式;(2)把x=﹣2代入抛物线解析式求出y的值,确定出D坐标,由OA为底,D纵坐标绝对值为高,求出三角形AOD面积即可.
-
科目: 来源: 题型:
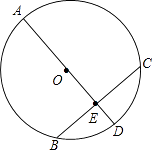
查看答案和解析>>【题目】如图,已知AD是⊙O的直径,BC是⊙O的弦,AD⊥BC,垂足为点E,AE=BC=16,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月完工的上海中心大厦是一座超高层地标式摩天大楼,其高度仅次于世界排名第一的阿联酋迪拜大厦,某人从距离地面高度263米的东方明珠球体观光层测得上海中心大厦顶部的仰角是22.3°.已知东方明珠与上海中心大厦的水平距离约为900米,那么上海中心大厦的高度约为米(精确到1米).(参考数据:sin22.3°≈0.38,cos22.3°≈0.93.tan22.3°≈0.41)
-
科目: 来源: 题型:
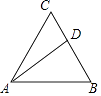
查看答案和解析>>【题目】如图,已知△ABC是边长为2的等边三角形,点D在边BC上,将△ABD沿着直线AD翻折,点B落在点B1处,如果B1D⊥AC,那么BD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,设
 =
= 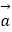 ,
, 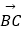 =
=  .
. 
(1)求向量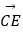 (用向量
(用向量 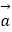 ,
,  的式子表示).
的式子表示).
(2)在图中作出向量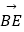 在向量
在向量 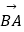 ,
, 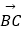 方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量). -
科目: 来源: 题型:
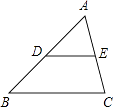
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.

(1)如果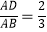 ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据
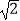 ≈1.41,
≈1.41, 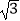 ≈1.73.
≈1.73. 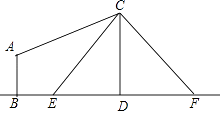
相关试题

