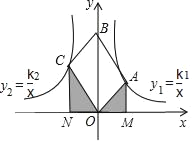
【题目】如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y1=![]() 和y2=
和y2=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ②阴影部分面积是
②阴影部分面积是![]() (k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
(k1﹣k2)③当∠AOC=90°时,|k1|=|k2|;④若四边形OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是_____.
参考答案:
【答案】①②④.
【解析】
作AE⊥y轴于点E,CF⊥y轴于点F,根据平行四边形的性质得S△AOB=S△COB,利用三角形面积公式得到AE=CF,则有OM=ON,再利用反比例函数k的几何意义和三角形面积公式得到S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=ONCN,所以有
|k2|=ONCN,所以有![]() ;由S△AOM=
;由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影=S△AOM+S△CON=
|k2|,得到S阴影=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
(k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
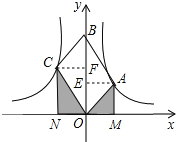
作AE⊥y轴于E,CF⊥y轴于F,如图,
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,
ONCN,
∴![]() ,故①正确;
,故①正确;
∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,
|k2|,
∴S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故②正确;
(k1-k2),故②正确;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确,
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式,你发现了什么规律?
12=
 ;12+22=
;12+22= ;12+22+32 =
;12+22+32 =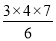 ; 12+22 +32 + 42 =
; 12+22 +32 + 42 = ;…
;…1)你能用一个算式表示这个规律吗?
2)根据你发现的规律,计算下面算式的值;
12+22 +32 + … +82
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(﹣2,y1)、(﹣1,y2)和(1,y3)分别在反比例函数y=﹣
 的图象上,则下列判断中正确的是( )
的图象上,则下列判断中正确的是( )A. y1<y2<y3 B. y3<y1<y2 C. y2<y3<y1 D. y3<y2<y1
-
科目: 来源: 题型:
查看答案和解析>>【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
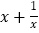 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是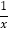 ,矩形的周长是2(
,矩形的周长是2(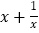 );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=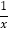 (x>0),解得x=1,这时矩形的周长2(
(x>0),解得x=1,这时矩形的周长2(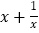 )=4最小,因此
)=4最小,因此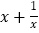 (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子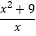 (x>0)的最小值是( )
(x>0)的最小值是( )A. 2 B. 1 C. 6 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】南江县在“创国家级卫生城市”中,朝阳社区计划对某区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川苍溪小王家今年红心猕猴桃喜获丰收,采摘上市20天全部销售完,小王对销售情况进行跟踪记录,并将记录情况绘制成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图(1)所示,红星猕猴桃的价格z(单位:元/千克)与上市时间x(天)的函数关系式如图(2)所示.
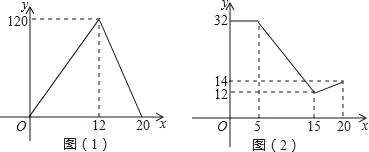
(1)观察图象,直接写出日销售量的最大值;
(2)求小王家红心猕猴桃的日销量y与上市时间x的函数解析式;并写出自变量的取值范围.
(3)试比较第6天和第13天的销售金额哪天多?
-
科目: 来源: 题型:
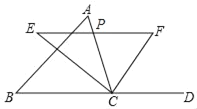
查看答案和解析>>【题目】如图,△ABC中,点P是AC边上一个动点,过P作直线EF∥BC,交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F.
(1)请说明:PE=PF;
(2)当点P在AC边上运动到何处时,四边形AECF是矩形?为什么?
相关试题

