【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?
参考答案:
【答案】(1)yA=16(1-x)2,、yB=12(1-x) (1+2x);
(2)当yA=yB时, x的值是![]() ;
;
(3)当x=![]() 时,三月份A、B两厂产值的差距最大,最大值是8.1万元
时,三月份A、B两厂产值的差距最大,最大值是8.1万元
【解析】
试题(1)根据A厂三月份产值=一月份产值×(1-x),代入数值即可;B厂三月份产值=一月份产值×(1-x) (1+2x).
(2)由 yA=yB得16(1-x)2=12(1-x) (1+2x),解得即可.
(3) 分析得到三月份A、B两厂产值的差距为yB-yA, 根据二次函数的性质即可求出.
试题解析:
(1)yA=16(1-x)2, yB=12(1-x) (1+2x).
(2)由题意得 16(1-x)2=12(1-x) (1+2x)
解得:x1=![]() , x2=1.
, x2=1.
∵0<x<1,∴x=![]() .
.
(3)当0<x<![]() 时,yA>yB,且0<yA-yB<4.
时,yA>yB,且0<yA-yB<4.
当![]() <x<1时,yB>yA,
<x<1时,yB>yA,
yB-yA=12(1-x) (1+2x)-16(1-x)2=4(1-x)(10x-1)=-40![]()
∵-40<0,![]() <x<1 ,
<x<1 ,
∴当x=![]() 时, yB-yA取最大值,最大值为8.1.
时, yB-yA取最大值,最大值为8.1.
∵8.1>4
∴当x=![]() 时,三月份A、B两厂产值的差距最大,最大值是8.1万元.
时,三月份A、B两厂产值的差距最大,最大值是8.1万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.
(1)若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为 ;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,
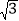 ≈1.72).
≈1.72).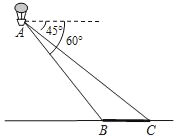
-
科目: 来源: 题型:
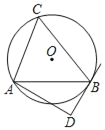
查看答案和解析>>【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣
 (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b, )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;
(2)如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
(3)如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出
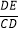 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.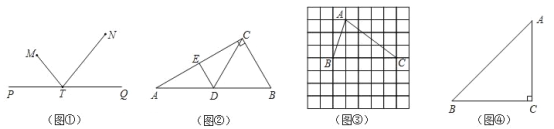
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=
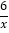 (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )
A. y=﹣
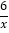 B. y=﹣
B. y=﹣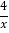 C. y=﹣
C. y=﹣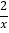 D. y=
D. y=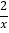
相关试题

