搜索
【题目】如果在一个斜坡上每向上前进13米，水平高度就升高了5米，则该斜坡的坡度i=
参考答案：
【答案】1：2.4
【解析】解：设在一个斜坡上前进13米，水平高度升高了5米，此时水平距离为x米， 根据勾股定理，得x2+52=132 ，
解得：x=12，
故该斜坡坡度i=5：12=1：2.4．
所以答案是：1：2.4．
【考点精析】本题主要考查了关于坡度坡角问题的相关知识点，需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程x2+ax﹣2a＝0的一个根是3，则它的另一根是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果“节约10%”记作+10%，那么“浪费6%”记作：
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
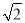CD，从而得出结论：AC+BC=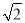CD．简单应用：
（1）在图①中，若AC=
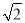，BC=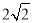
，则CD= ．（2）如图③，AB是⊙O的直径，点C、D在⊙上，
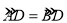，若AB=13，BC=12，求CD的长．拓展规律：
（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）
（4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE=
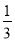AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】按四舍五入法则取近似值：
2.086≈ （精确到百分位）．
0.03445≈ （精确到0.001） -
科目： 来源： 题型：
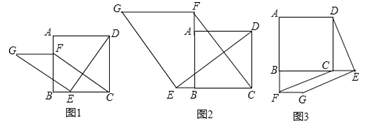
查看答案和解析>>【题目】如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．
（1）请判断：FG与CE的数量关系是 ，位置关系是 ；
（2）如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；
（3）如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各变形中，不正确的是（ ）
A. 从x+3=6，可得x=6﹣3
B. 从2x=x﹣2，可得2x﹣x=﹣2
C. 从x+1=2x，可得x﹣2x=1
D. 从2x﹣4=3x+8，可得2x﹣3x=8+4
相关试题
