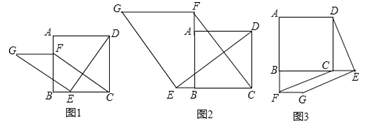
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是 ,位置关系是 ;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
参考答案:
【答案】(1)FG=CE,FG∥CE;(2)成立;(3)成立.
【解析】
试题分析:(1)只要证明四边形CDGF是平行四边形即可得出FG=CE,FG∥CE;
(2)构造辅助线后证明△HGE≌△CED,利用对应边相等求证四边形GHBF是矩形后,利用等量代换即可求出FG=C,FG∥CE;
(3)证明△CBF≌△DCE后,即可证明四边形CEGF是平行四边形.
试题解析:(1)FG=CE,FG∥CE;
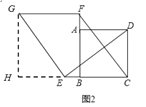
(2)过点G作GH⊥CB的延长线于点H,∵EG⊥DE,∴∠GEH+∠DEC=90°,∵∠GEH+∠HGE=90°,∴∠DEC=∠HGE,在△HGE与△CED中,∵∠GHE=∠DCE,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED(AAS),∴GH=CE,HE=CD,∵CE=BF,∴GH=BF,∵GH∥BF,∴四边形GHBF是矩形,∴GF=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=EC,∴FG=EC;
(3)∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°,在△CBF与△DCE中,∵BF=CE,∠FBC=∠ECD,BC=DC,∴△CBF≌△DCE(SAS),∴∠BCF=∠CDE,CF=DE,∵EG=DE,∴CF=EG,∵DE⊥EG,∴∠DEC+∠CEG=90°,∵∠CDE+∠DEC=90°,∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=
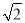 CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=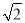 CD.
CD.简单应用:
(1)在图①中,若AC=
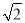 ,BC=
,BC=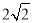 ,则CD= .
,则CD= .(2)如图③,AB是⊙O的直径,点C、D在⊙上,
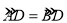 ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=
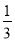 AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果在一个斜坡上每向上前进13米,水平高度就升高了5米,则该斜坡的坡度i=
-
科目: 来源: 题型:
查看答案和解析>>【题目】按四舍五入法则取近似值:
2.086≈ (精确到百分位).
0.03445≈ (精确到0.001) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各变形中,不正确的是( )
A. 从x+3=6,可得x=6﹣3
B. 从2x=x﹣2,可得2x﹣x=﹣2
C. 从x+1=2x,可得x﹣2x=1
D. 从2x﹣4=3x+8,可得2x﹣3x=8+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们学过的全等变换方式有、、,生活中常用这三种图形变换进行图案设计.在图形的上述变换过程中,其和不变,只是发生了改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果式子﹣2x﹣6的值等于﹣2,则x的值是( )
A. ﹣2 B. 2 C. ﹣3 D. 3
相关试题

