【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

参考答案:
【答案】4n+3
【解析】
利用给出的三个图形寻找规律,发现白色正方形个数=总的正方形个数-黑色正方形个数,而黑色正方形个数第1个为1,第二个为2,由此寻找规律,总个数只要找到边与黑色正方形个数之间关系即可,依此类推,寻找规律.
解:方法一:
第1个图形黑、白两色正方形共3×3个,其中黑色1个,白色3×3-1个,
第2个图形黑、白两色正方形共3×5个,其中黑色2个,白色3×5-2个,
第3个图形黑、白两色正方形共3×7个,其中黑色3个,白色3×7-3个,
依此类推,
第n个图形黑、白两色正方形共3×(2n+1)个,其中黑色n个,白色3×(2n+1)-n个,
即:白色正方形5n+3个,黑色正方形n个,
故第n个图案中白色正方形比黑色正方形多4n+3个,
方法二
第1个图形白色正方形共8个,黑色1个,白色比黑色多7个,
第2个图形比第1个图形白色比黑色又多了4个,即白色比黑色多(7+4)个,
第3个图形比第2个图形白色比黑色又多了4个,即白色比黑色多(7+4×2)个,
类推,第n个图案中白色正方形比黑色正方形多[7+4(n-1)]个,即(4n+3)个,
故第n个图案中白色正方形比黑色正方形多4n+3个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)又一个“六一”国际儿童节即将到来,学校打算给初一的学生赠送精美文具包,文具店规定一次购买400个以上,可享受8折优惠.若给初一学生每人购买一个,则不能享受优惠,需付款1936元;若多买88个,则可享受优惠,同样只需付款1936元,该校初一年级学生共有多少人?
(2)初一(1)班为准备六一联欢会,欲购买价格分别为4元、8元和20元的三种奖品,每种奖品至少购买一件,共买16件,恰好用100元.若4元的奖品购买a件,先用含a的代数式表示另外两种奖品的件数,然后设计可行的购买方案.
作为初二的大哥哥、大姐姐,你会解决这两个问题吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
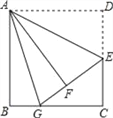
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(操作观察)任意一张三角形纸片有3个顶点。
第1次在它的内部增画1个点,此时三角形纸片内部共有1个点;
第2次在它的内部继续增画2个点,此时三角形纸片内部共有1+2=3个点;
第3次在它的内部继续增画3个点,此时三角形纸片内部共有1+2+3=6个点;
……
第
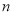 次在它的内部继续增画
次在它的内部继续增画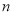 个点,此时三角形纸片内部共有
个点,此时三角形纸片内部共有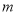 个点。
个点。(动手实践)
第
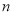 次画点后,在三角形纸片内部共有
次画点后,在三角形纸片内部共有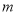 个点,以
个点,以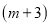 个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得
个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得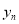 个这样的小三角形。
个这样的小三角形。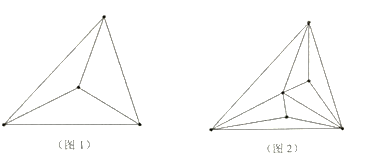
(思考解答)
(1)第
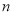 次画点后,
次画点后,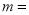 __________________;(用含有
__________________;(用含有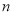 的代数式表示);
的代数式表示);(2)第1次画点后,如图1,以4个点为顶点,将原三角形纸片剪成若干个小三角形,最多可以剪得3个这样的小三角形,所以
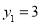 ;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以
;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以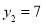 ;第3次画点后,以9个点为顶点,可得
;第3次画点后,以9个点为顶点,可得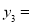 ____________________;
____________________;(3)第
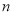 次画点后,可得
次画点后,可得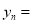 ______________;(用含有
______________;(用含有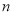 的代数式表示);
的代数式表示);(4)第
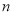 次画点后,可得
次画点后,可得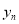 个小三角形,第
个小三角形,第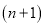 次画点后,可得
次画点后,可得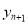 个小三角形,则
个小三角形,则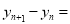 ________________________。(用含有
________________________。(用含有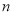 的代数式表示)。
的代数式表示)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)3(x﹣6)=12 ;
(2)x﹣
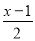 =2﹣
=2﹣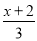
(3)
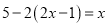 ;
;(4)
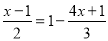
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.
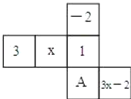
(1)求x的值.
(2)求正方体的上面和底面的数字和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=
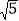 ,BD=2,求OE的长.
,BD=2,求OE的长.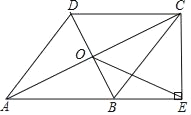
相关试题

