【题目】已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为 . 
参考答案:
【答案】(2,﹣4)
【解析】解:∵抛物线y=ax2+x的对称轴为直线x=2, ∴﹣ ![]() =2,
=2,
∴a=﹣ ![]() ,
,
∴抛物线的表达式为:y=﹣ ![]() x2+x,
x2+x,
∴顶点A的坐标为(2,1),
设对称轴与x轴的交点为E.
如图,在直角三角形AOE和直角三角形POE中,tan∠OAE= ![]() ,tan∠EOP=
,tan∠EOP= ![]() ,
,
∵OA⊥OP,
∴∠OAE=∠EOP,
∴ ![]() =
= ![]() ,
,
∵AE=1,OE=2,
∴ ![]() =
= ![]() ,
,
解得PE=4,
∴P(2,﹣4),
所以答案是:(2,﹣4).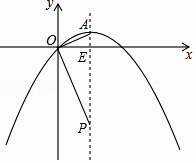
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12;第2次输出的结果是6;依次继续下去……第2018次输出的结果是_____.
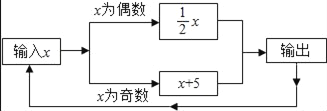
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)-2-(-3)+(-8); (2)(-16)÷
 ×(-
×(- );
);(3)
 ; (4)
; (4) ;
;(5)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能判定四边形ABCD为平行四边形的条件是
A.
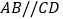 ,
,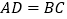 B.
B. 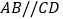 ,
,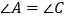
C.
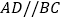 ,
,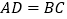 D.
D. 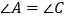 ,
,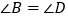
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其中三面留出宽都是x米的小路,中间余下的长方形部分做菜地.
(1)菜地的长a = 米,宽b= 米(用含x的代数式表示);
(2)菜地的面积S= 平方米(用含x的代数式表示);
(3)当x=1米时,求菜地的面积.

相关试题

