搜索
【题目】作图题：
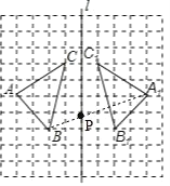
如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
（1）在图中画出△ABC关于直线l对称的△A1B1C1；
（要求：A与A1，B与B1，C与C1相对应）
（2）求出△A1B1C1面积．
（3）在直线l上找一点P，使得PA+PB的值最小.
参考答案：
【答案】（1）详见解析；（2）△ABC的面积：S△ABC=5；（3）连结AB1交l于点P，则使PA+PB=AB1的值最小，点P是所求作的点.
【解析】
（1）分别作出A、B、C关于l的对称点A1、B1、C1，再连接即可；
（2）利用割补法求解可得结果；
（3）根据两点之间线段最短，连接A1B交直线l于点P，点P即为所求.
(1)如图所示,△A1B1C1即为所求；
(2)采用割补法，梯形面积减去两个小直角三角形面积可得
△A1B1C1面积=
；
(3)如图，连接A1B交直线l于点P，点P即为所求.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A、B两组，采用不同工艺做降温对比实验，设降温开始后经过x min时，A、B两组材料的温度分别为yA℃、yB℃，yA、yB与x的函数关系式分别为yA=kx+b，yB=
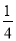（x﹣60）2+m（部分图象如图所示），当x=40时，两组材料的温度相同．
（1）分别求yA、yB关于x的函数关系式；
（2）当A组材料的温度降至120℃时，B组材料的温度是多少？
（3）在0＜x＜40的什么时刻，两组材料温差最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC，△DEC均为直角三角形，B，C，E三点在一条直线上，过D作DM⊥AC于M．
（1）如图1，若△ABC≌△DEC，且AB=2BC．
①过B作BN⊥AC于N，则线段AN，BN，MN之间的数量关系为： ；（直接写出答案）
②连接ME，求
的值； （2）如图2，若AB=CE=DE，DM=2，MC=1，求ME的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，抛物线
与x轴正半轴交于A、B两点（A点在B点左边），且AB=4．（1）求k值；
（2）该抛物线与直线
交于C、D两点，求S△ACD；（3）该抛物线上是否存在不同于A点的点P，使S△PCD=S△ACD？若存在，求出P点坐标．
（4）若该抛物线上有点P，使S△PCD=tS△ACD，抛物线上满足条件的P点有2个，3个，4个时，分别直接写出t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AB=AD=2，∠A=60°，BC=
，CD=3．
（1）求∠ADC的度数；
（2）求四边形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知△ABC,以AB、AC为边向△ABC外作等边三角形ABD和等边三角形ACE，连接BE、CD.请你完成图形，并证明：BE=CD;
（2）如图（2），已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,BE和CD有什么数量关系？说明理由；
（3）运用(1)(2)解答中所积累的经验和知识，完成下题：如图（3），要测量河两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=1千米，AC=AE.求BE的长.
相关试题
