Question

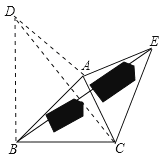
【题目】（1）如图（1），已知△ABC,以AB、AC为边向△ABC外作等边三角形ABD和等边三角形ACE，连接BE、CD.请你完成图形，并证明：BE=CD;

（2）如图（2），已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,BE和CD有什么数量关系？说明理由；

（3）运用(1)(2)解答中所积累的经验和知识，完成下题：如图（3），要测量河两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=1千米，AC=AE.求BE的长.

Answer 1

【答案】（1）详见解析；（2）BE=CD；（3）千米

【解析】

（1）利用等边三角形的性质，用边角边易证△CAD≌△EAB，即可得BE=CD;

（2）证法同（1），用边角边易证△CAD≌△EAB，可得结果；

（3）由（1）、（2）的解题经验可知，过A作等腰直角三角形ABD，连接CD，利用勾股定理求出BD，由题意得到△DBC为直角三角形，利用勾股定理求出CD，即为BE的长.

解：（1）∵△ABD和△ACE都是等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAE=60°.

∴∠BAD+∠BAC=∠CAE+∠BAC，

即 ∠CAD=∠EAB.

在△CAD和△EAB中，

，

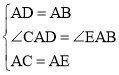∴△CAD≌△EAB（SAS）. ∴BE=CD

（2）BE=CD

理由同（1）：∵四边形ABFD和ACGE均为正方形，

∴AD=AB，AC=AE，∠BAD=∠CAE=90°.∴∠CAD=∠EAB.

∵在△CAD和△EAB中：

AD=AB，∠CAD=∠EAB，AC=AE

∴△CAD≌△EAB（SAS），∴BE=CD

（3）由（1）、（2）的解题经验可知，过A作等腰直角三角形ABD，∠BAD=90°，连接CD，

则AD=AB=1千米，∠ABD=45°，∴千米.

连接CD，则由（2）可得BE=CD.

∵∠ABC=45°，∴∠DBC=90°.

在Rt△DBC中，BC=1千米，千米，

根据勾股定理得：（千米）.

∴BE=CD=千米.