搜索
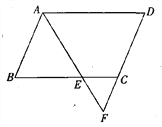
【题目】如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F．已知AB＝4，BC＝6，∠F＝55°，求线段EC的长和∠D的度数．
参考答案：
【答案】EC=2，∠D=70°
【解析】分析：根据平行四边形的性质可得AB∥CD， AD∥BC，再由平行线的性质和角平分线的定义证得∠BAE=∠AEB，根据等腰三角形的性质可得AB=BE=4，从而求得EC的长；根据平行线的性质以及三角形内角和定理求得∠D的度数即可．
详解：
在平行四边形ABCD中，AB∥CD， AD∥BC，
∵AD∥BC ，
∴∠DAE=∠AEB，
∵AF平分∠BAD，
∴∠DAE=∠BAE，
∴∠BAE=∠AEB ，
∴AB=BE=4，
∴EC=6-4=2；
∵AB∥CD，
∴∠BAE=∠F，
∴∠DAE=∠F=55°，
∴∠D=70°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系
的原点O在格点上， 
轴、
轴都在网格线上．线段AB的端点A、B在格点上．
（1）将线段AB绕点O逆时针90°得到线段A1B1，请在图中画出线段A1B1；
（2）在（1）的条件下，线段A2B2与线段A1B1关于原点O成中心对称，请在图中画出线段A2B2；
（3）在（1）、（2）的条件下，点P是此平面直角坐标系内的一点，当以点A、B、B2、P为顶点的四边形是平行四边形时，请直接写出点P的坐标： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为（﹣1，0），则一元二次方程ax2﹣2ax+c=0的根为
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动，它从A处出发看望B、C、D处的其它甲虫．规定：向上向右走为正，向下向左走为负，如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)．其中第一数表示左右方向，第二个数表示上下方向，那么图中
(1)A→C( ， )，B→D( ， )；
(2)若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D是AB的中点，E是AC上一点，EF∥AB， DF∥BE．请你猜想DF与AE的关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下面一列数，探求其规律：
，－
，
，－
，
，－
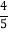，…(1) 写出第7，8，9项的三个数；
(2) 第2 018个数是什么？
(3) 如果这一列数无限排列下去，与 ____ 、____ 两数越来越接近？
-
科目： 来源： 题型：
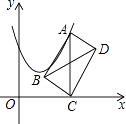
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为
相关试题
