【题目】已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为(﹣1,0),则一元二次方程ax2﹣2ax+c=0的根为
参考答案:
【答案】﹣1,3
【解析】解法一:将x=﹣1,y=0代入y=ax2﹣2ax+c得:a+2a+c=0.
解得:c=﹣3a.
将c=﹣3a代入方程得:ax2﹣2ax﹣3a=0.
∴a(x2﹣2x﹣3)=0.
∴a(x+1)(x﹣3)=0.
∴x1=﹣1,x2=3.
解法二:已知抛物线的对称轴为x= ![]() =1,又抛物线与x轴一个交点的坐标为(﹣1,0),则根据对称性可知另一个交点坐标为(3,0);故而ax2﹣2ax+c=0的两个根为﹣1,3
=1,又抛物线与x轴一个交点的坐标为(﹣1,0),则根据对称性可知另一个交点坐标为(3,0);故而ax2﹣2ax+c=0的两个根为﹣1,3
所以答案是:﹣1,3.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某校开展了“书香校园”、“书香家庭”的活动.学校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:


(1)这次随机调查了 名学生,统计表中d= ;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是 °;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系
 的原点O在格点上,
的原点O在格点上,  轴、
轴、 轴都在网格线上.线段AB的端点A、B在格点上.
轴都在网格线上.线段AB的端点A、B在格点上.
(1)将线段AB绕点O逆时针90°得到线段A1B1,请在图中画出线段A1B1;
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2;
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形是平行四边形时,请直接写出点P的坐标: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4).其中第一数表示左右方向,第二个数表示上下方向,那么图中

(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
-
科目: 来源: 题型:
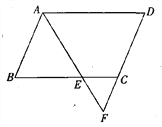
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.已知AB=4,BC=6,∠F=55°,求线段EC的长和∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是AB的中点,E是AC上一点,EF∥AB, DF∥BE.请你猜想DF与AE的关系,并说明理由.

相关试题

