【题目】如图,二次函数y=ax2+bx+c的图像经过点A(-1,0),点B(3,0),交y轴正半轴于点C,给出下列结论:
①a=-1, b=2, c=3;
②若0<x<4,则5a<y<-3a;
③对任意实数m,一定有am2+bm+a≤0;
④一元二次方程cx2+bx+a=0的两个根为-1和![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①③ B. ②③ C. ②④ D. ③④
参考答案:
【答案】D
【解析】
利用交点式写出抛物线解析式为y=ax2-2ax-3a,则可对①进行判断;配成顶点式得y=a(x-1)2-4a,计算x=4时,y=a51=5a,则根据二次函数的性质可对②进行判断;根据顶点式,抛物线向下平移-4a个单位,解析式为:y′=ax2+bx+c+4a=ax2+bx-3a+4a=ax2+bx+a≤0,可对③进行判断;由于b=-2a,c=-3a,则方程cx2+bx+a=0化为-3ax2-2ax+a=0,然后解方程可对④进行判断.
∵二次函数y=ax2+bx+c的图象经过点A(-1,0),点B(3,0),
∴抛物线解析式为y=a(x+1)(x-3),即y=ax2-2ax-3a,
∴b=-2a,c=-3a,
∴a:b:c=-1:2:3,故①错误;
当x=4时,y=a(x+1)(x-3)=a51=5a,y=ax2-2ax-3a=a[(x-1)2-4]=a(x-1)2-4a,
∴当0<x<4时,则5a<y<-4a,所以②错误;
∵y=ax2-2ax-3a=a[(x-1)2-4]=a(x-1)2-4a,
∴顶点坐标为(1,-4a),
∵抛物线开口向下,c=-3a,
∴抛物线向下平移-4a个单位,则抛物线顶点为(1,0),
∴平移后的解析式为:y′=ax2+bx+c+4a=ax2+bx-3a+4a=ax2+bx+a≤0,故③正确;
∵b=-2a,c=-3a,
∴方程cx2+bx+a=0化为-3ax2-2ax+a=0,
整理得3x2+2x-1=0,解得x1=-1,x2=![]() ,所以④正确.
,所以④正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=
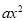 +bx﹣4经过A(﹣4,0),C(2,0)两点.
+bx﹣4经过A(﹣4,0),C(2,0)两点.(1)求抛物线的解析式;
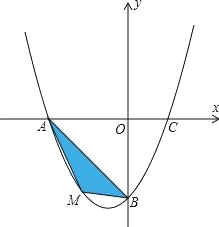
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量
 (mg)与燃烧时间
(mg)与燃烧时间 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,  与
与 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:(1)求药物燃烧时
 与
与 的函数关系式.(2)求药物燃烧后
的函数关系式.(2)求药物燃烧后 与
与 的函数关系式.
的函数关系式.(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是



A. 55° B. 60° C. 65° D. 70°
-
科目: 来源: 题型:
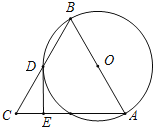
查看答案和解析>>【题目】已知在△ABC中,AB=CB,以AB为直径的⊙O交于点D,过D作⊙O的切线交AC于E,且DE⊥AC,则∠C的度数为=_________________.
-
科目: 来源: 题型:
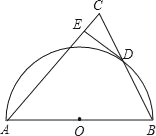
查看答案和解析>>【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
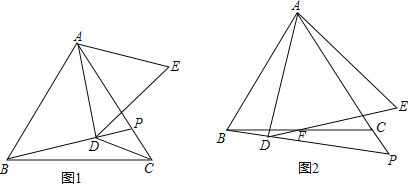
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则
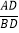 = ;(直接写结果)
= ;(直接写结果)(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=
 ,请直接写出CP的长 .
,请直接写出CP的长 .
相关试题

