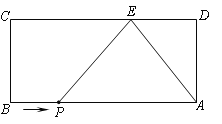
【题目】如图,长方形ABCD,AB=9,AD=4. E为CD边上一点,CE=6.
(1)求AE的长.
(2)点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE. 设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?
参考答案:
【答案】3或4或![]()
【解析】试题分析:(1)求出DE=3,AD=4,利用勾股定理即可求出AE的长;
(2)根据若△PAE为等腰三角形,分三种情况讨论:当EP=EA时;当AP=AE时;当PE=PA时.
试题解析:
(1)在长方形ABCD中,∠D=90°,CD=AB=9
在Rt△ADE中,DE=9-6=3,AD=4,
∴AE=5
(2)若△PAE为等腰三角形,则有三种可能.
当EP=EA时,AP=6,
∴t=BP=3
当AP=AE时,则9-t=5,
∴t=4
当PE=PA时,则(6-t)2+42=(9-t)2,
∴t=![]()
综上所述,符合要求的t值为3或4或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
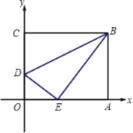
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲地与丙地由公路连接,乙地在甲、丙两地之间,一辆汽车在下午1点钟从离甲地10千米的M地出发向乙地匀速前进,15分钟后离甲地20千米,当汽车行驶到离甲地150千米的乙地时,接到通知要在下午5点前赶到离乙地30千米的丙地.汽车若按原速能否按时到达?若能,是在几点几时到达;若不能,车速应提高到多少才能按时到达?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
 ﹣1的步骤如下:
﹣1的步骤如下:(解析)第一步:
 ﹣1(分数的基本性质)
﹣1(分数的基本性质)第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣
 ……(⑤)
……(⑤)以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2), 
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两城市相距80km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:
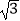 ≈1.732,
≈1.732, 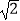 ≈1.414)
≈1.414)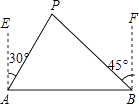
相关试题

