【题目】如图,已知函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且与
,且与![]() 的图像交于点
的图像交于点![]() .
.

(1)求![]() 的值;
的值;
(2)若![]() ,则
,则![]() 的取值范围是 ;
的取值范围是 ;
(3)求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)m=-1,b=2;(2) x>-1;(3)11
【解析】
(1)先由函数y1=x+5,求出点A,点D的坐标,得到m的值;再将D点坐标代入y2=-2x+b,求出b的值;
(2)根据函数图象,求出y1落在y2图象上方的部分对应的x的取值范围即可;
(3)先由y2=-2x+2,求出B,C两点的坐标,再代入S四边形AOCD=S△ABD-S△BOC计算即可.
(1)∵函数y1=x+5的图象与x轴交于点A,
∴A(-5,0).
∵y=4时,x+5=4,解得x=-1,
∴D(-1,4).
将D(-1,4)代入y2=-2x+b,
得4=-2×(-1)+b,
解得b=2,
故m=-1,b=2;
(2)由图象可知,若y1>y2,则x的取值范围是x>-1.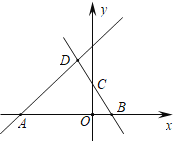
故答案为x>-1;
(3)∵一次函数y2=-2x+2的图象分别与x轴、y轴交于点B,C,
∴B(1,0),C(0,2),
∴S四边形AOCD=S△ABD-S△BOC
=![]() ×6×4-
×6×4-![]() ×1×2
×1×2
=12-1
=11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
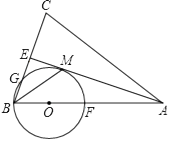
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,,ED交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有( )

A. ②③B. ①②③C. ①③④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的增强,“低碳出行”越来越为人们所倡导。小李要从家乡到宁波工作,若乘飞机需要3小时,乘汽车需要9小时。这两种交通工具每小时排放的二氧化碳总量为80千克,已知飞机每小时二氧化碳的排放量比汽车多46千克,若小李乘汽车来宁波,那么他此行与乘飞机相比将减少二氧化碳排放量多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A. ﹣
﹣  =15
=15
B. ﹣
﹣  =
= 
C. ﹣
﹣  =15
=15
D. ﹣
﹣  =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A.13
B.14
C.15
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型
B型
价格(万元/台)
12
10
月污水处理能力(吨/月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
相关试题

