【题目】对于平面内任意一个角的“夹线圆”,给出如下定义:如果一个圆与这个角的两边都相切,则称这个圆为这个角的“夹线圆”.例如:在平面直角坐标系xOy中,以点(1,1)为圆心,1为半径的圆是x轴与y轴所构成的直角的“夹线圆”.
(1)下列各点中,可以作为x轴与y轴所构成的直角的“夹线圆”的圆心的点是哪些;
A(2,2),B(3,1),C(-1,0),D(1,-1)
(2)若⊙P为y轴和直线 l:![]() 所构成的锐角的“夹线圆”,且⊙P的半径为1,求点P的坐标.
所构成的锐角的“夹线圆”,且⊙P的半径为1,求点P的坐标.
(3)若 ⊙Q为x轴和直线![]() 所构成的锐角的“夹线圆”,且⊙Q的半径
所构成的锐角的“夹线圆”,且⊙Q的半径![]() ,直接写出点Q横坐标
,直接写出点Q横坐标![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)A,D; (2)P点坐标为![]() ,
,![]() (3)
(3)![]()
【解析】
(1)由点A的横纵坐标相等及点D的横纵坐标的绝对值相等,可得出点A,D能作为x轴与y轴所构成的直角的“夹线圆”的圆心;
(2)过P点作PE⊥y轴于点E,PF⊥直线l于点F,连PO,设直线l与x轴夹角为α,由直线l的解析式可得出α=30°及∠EOF=60°,由⊙P与y轴及直线OF均相切可得出∠EOP=30°,结合EP=1可求出OE=![]() ,进而可得出点E的坐标;
,进而可得出点E的坐标;
(3)过Q点作QM⊥x轴于点M,QN⊥直线y=-![]() x+2
x+2![]() 于点N,延长MQ交直线y=-
于点N,延长MQ交直线y=-![]() x+2
x+2![]() 于点G,设直线y=-
于点G,设直线y=-![]() x+2
x+2![]() 与x轴交于点S,利用一次函数图象上点的坐标特征可得出点S的坐标,由∠MSG=30°,∠MGS=60°可得出MS=MGtan60°=(2+
与x轴交于点S,利用一次函数图象上点的坐标特征可得出点S的坐标,由∠MSG=30°,∠MGS=60°可得出MS=MGtan60°=(2+![]() )r,结合1≤r≤2可得出MS的取值范围,再将其代入xQ=6+MS或xQ=6-MS即可得出点Q横坐标xQ的取值范围.
)r,结合1≤r≤2可得出MS的取值范围,再将其代入xQ=6+MS或xQ=6-MS即可得出点Q横坐标xQ的取值范围.
(1))∵2=2,1=|-1|,
∴点A,D能作为x轴与y轴所构成的直角的“夹线圆”的圆心.
故答案为:点A, D能作为x轴与y轴所构成的直角的“夹线圆”的圆心.
(2)如图:过P点作PA⊥y轴于点A,PB⊥l于B,连PO.
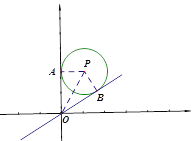
∵点B为直线![]() 上一点
上一点
∴设B点坐标为(x,![]() )
)
设直线![]() 与x轴夹角为
与x轴夹角为![]()
![]()
∴直线 l与x轴的夹角为30°
∴∠AOB=60°
又∵⊙P与x轴及直线OB均相切,
∴OP平分∠AOB
∴∠AOP=30°
又∵AP=1
∴P点坐标为![]()
同理,当P点在第三象限时,P点坐标为![]()
(3)![]()
理由:如图2,过Q点作QM⊥x轴于点M,QN⊥直线y=-![]() x+2
x+2![]()
于点N,延长MQ交直线y=-![]() x+2
x+2![]() 于点G,设直线y=-
于点G,设直线y=-![]() x+2
x+2![]() 与x轴交于点S.
与x轴交于点S.
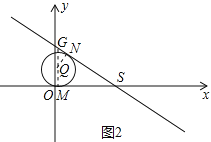
当y=0时,有-![]() x+2
x+2![]() =0,
=0,
解得:x=6,
∴点S的坐标为(6,0).
∵∠MSG=30°,
∴∠MGS=60°,
∴MG=MQ+QG=r+![]() =
=![]() r ,
r ,
∴MS=MGtan60°=(2+![]() )r,
)r,
∵⊙Q的半径1≤r≤2,
∴2+![]() ≤MS≤4+2
≤MS≤4+2![]() ,
,
∴2-2![]() ≤6-MS≤4-
≤6-MS≤4-![]() ,8+
,8+![]() ≤6+MS≤10+2
≤6+MS≤10+2![]() ,
,
∴点Q横坐标xQ的取值范围为:2-2![]() ≤xQ≤4-
≤xQ≤4-![]() 或8+
或8+![]() ≤xQ≤10+2
≤xQ≤10+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是⊙O直径AB上一点,过C作CD⊥AB交⊙O于点D,连接DA,延长BA至点P,连接DP,使∠PDA=∠ADC.
(1)求证:PD是⊙O的切线;
(2)若AC=3,tan∠PDC=
 ,求BC的长.
,求BC的长.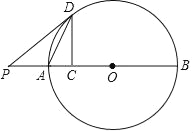
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
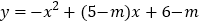 .
.(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线
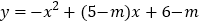 与
与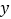 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线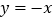 的对称点恰好是点M,求
的对称点恰好是点M,求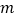 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点E为线段AB上一动点(不与点A,B重合),连接CE,将∠ACE的两边CE,CA分别绕点C顺时针旋转90°,得到射线CE,,CA,,过点A作AB的垂线AD,分别交射线CE,,CA,于点F,G.
(1)依题意补全图形;
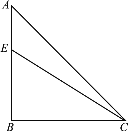
(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示);
(3)用等式表示线段AE,AF与BC之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表给出了以下结论:
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
12
5
0
﹣3
﹣4
﹣3
0
5
12
…
①二次函数y=ax2+bx+c有最小值,最小值为﹣3;②当﹣
 <x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )
<x<2时,y<0;③二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴的两侧;④当x<1时,y随x的增大而减小.则其中正确结论有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=
 DE.
DE.①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

相关试题

