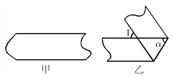
【题目】(1)有一条纸带如图甲所示,怎样检验纸带的两条边线是否平行?说明你的方法和理由.
(2)如图乙,将一条上下两边互相平行的纸带折叠,设∠1为x度,请用x的代数式表示∠α的度数.
参考答案:
【答案】(1)见解析;(2)∠α=∠3=90°-![]() x°
x°
【解析】整体分析:
(1)将纸条如图折叠后,度量所成的同位角是否相等或内错角是否相等或同旁内角是否相等;(2)先判断纸条的重叠部分是等腰三角形,再用三角形的内角和定理计算.
解:(1)(方法不唯一)如图1,将纸条如图折叠,测得∠1=∠2,于是根据同位角相等,两直线平行得到纸带的两条边线是平行的;

(2)如图2,∵AB∥CD,∴∠2=∠1=x°,∠3=∠α,∵将一条上下两边互相平行的纸带折叠,∴∠3=∠4=![]() (180°-∠2)=90°-
(180°-∠2)=90°-![]() ∠2=90°-
∠2=90°-![]() x°,∴∠α=∠3=90°-
x°,∴∠α=∠3=90°-![]() x°.
x°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P,Q分别是双曲线
 在第一、三象限上的点,PA⊥
在第一、三象限上的点,PA⊥ 轴,QB⊥
轴,QB⊥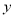 轴,垂足分别为A,B,点C是PQ与
轴,垂足分别为A,B,点C是PQ与 轴的交点.设△PAB的面积为
轴的交点.设△PAB的面积为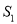 ,△QAB的面积为
,△QAB的面积为 ,△QAC的面积为
,△QAC的面积为 ,则有( )
,则有( )
A.
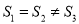 B.
B.  C.
C. 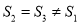 D.
D. 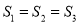
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结 CD,EB.
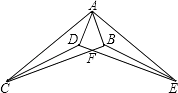
(1)不添加辅助线,找出图中其它的全等三角形;
(2)求证:CF=EF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE,CD相交于点F,求证:∠CEF=∠CFE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a3+ a 3=4 a 6B.( a +b)2= a 2+b2C.5 a-5 a =0 D.(-a)2·a 3=-a 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】x<0,y>0时,则x,x+y,x﹣y,y中最小的数是( )
A.x
B.x﹣y
C.x+y
D.y
相关试题

