【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
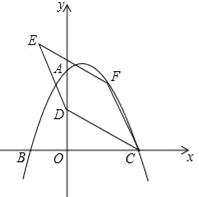
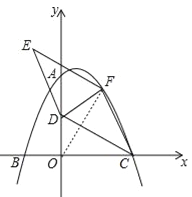
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
参考答案:
【答案】(1)![]() ,C(8,0);(2)①50;②18.
,C(8,0);(2)①50;②18.
【解析】
试题分析:(1)把A点和B点坐标代入![]() 得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
(2)①连结OF,如图,设F(t,![]() ),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=
),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=![]() ,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),然后把E(t﹣8,
),然后把E(t﹣8,![]() )代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
试题解析:(1)把A(0,8),B(﹣4,0)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,所以抛物线的解析式为
,所以抛物线的解析式为![]() ;
;
当y=0时,![]() ,解得
,解得![]() ,
,![]() ,所以C点坐标为(8,0);
,所以C点坐标为(8,0);
(2)①连结OF,如图,设F(t,![]() ),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=
),∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,∴S△CDF=S△ODF+S△OCF﹣S△OCD=![]() =
=![]() =
=![]() ;
;
当t=3时,△CDF的面积有最大值,最大值为25,∵四边形CDEF为平行四边形,∴S的最大值为50;
②∵四边形CDEF为平行四边形,∴CD∥EF,CD=EF,∵点C向左平移8个单位,再向上平移4个单位得到点D,∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(t﹣8,![]() ),∵E(t﹣8,
),∵E(t﹣8,![]() )在抛物线上,∴
)在抛物线上,∴ ![]() ,解得t=7,当t=7时,S△CDF=
,解得t=7,当t=7时,S△CDF=![]() =9,∴此时S=2S△CDF=18.
=9,∴此时S=2S△CDF=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣2,4)关于坐标原点对称的点的坐标为( )
A. (4,﹣2)B. (﹣4,2)C. (2,4)D. (2,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016江西省)设抛物线的解析式为
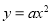 ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点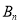 (
(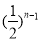 ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点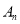 ,连接
,连接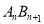 ,得直角三角形
,得直角三角形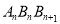 .
.(1)求a的值;
(2)直接写出线段
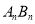 ,
,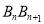 的长(用含n的式子表示);
的长(用含n的式子表示);(3)在系列Rt△
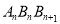 中,探究下列问题:
中,探究下列问题:①当n为何值时,Rt△
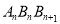 是等腰直角三角形?
是等腰直角三角形?②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△
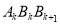 与Rt△
与Rt△ 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式减去﹣2m结果等于m2+3m+2,这个多项式是( )
A.m2+5m+2
B.m2﹣m﹣2
C.m2﹣5m﹣2
D.m2+m+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(x﹣1)2,下列结论正确的是( )
A. 当x>0时,y随x的增大而减小B. 当x<0时,y随x的增大而增大
C. 当x<1时,y随x的增大而减小D. 当x<﹣1时,y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】把91000写成a×10n(1≤a<10,n为整数)的形式,则a=( )
A. 9 B. ﹣9 C. 0.91 D. 9.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=x2﹣4x+3的图象沿y轴向下平移1个单位长度,再沿x轴向左平移3个单位长度后,此时抛物线相应的函数表达式是_____.
相关试题

