【题目】解答题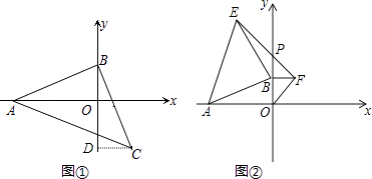
(1)如图①,等腰直角△ABC中,∠ABC=90°,AB=BC,点A、B分别在坐标轴上,若点C的横坐标为2,直接写出点B的坐标;(提示:过C作CD⊥y轴于点D,利用全等三角形求出OB即可)
(2)如图②,若点A的坐标为(﹣6,0),点B在y轴的正半轴上运动时,分别以OB、AB为边在第一、第二象限作等腰直角△OBF,等腰直角△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值.若变化,求PB的取值范围.
参考答案:
【答案】
(1)(0,2)
(2)
解:PB的长度不发生改变,
理由:如图3,作EG⊥y轴于G,
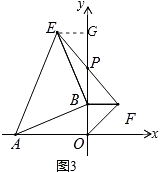
∵∠BAO+∠OBA=90°,∠OBA+∠EBG=90°,
∴∠BAO=∠EBG,
在△BAO和△EBG中, 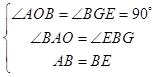
∴△BAO≌△EBG(AAS),
∴BG=AO,EG=OB,
∵OB=BF,
∴BF=EG,
在△EGP和△FBP中, 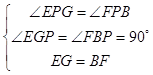 ,
,
∴△EGP≌△FBP(AAS),
∴PB=PG,
∴PB= ![]() BG=
BG= ![]() AO=3
AO=3
即:PB的长度不发生改变,是定值为3.
【解析】解:(1)如图1,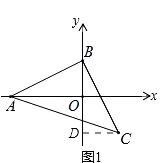
作CD⊥BO于D,
∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中,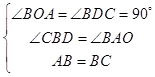 ,
,
∴△ABO≌△BCD(AAS),
∴CD=BO=2,
∴B点坐标(0,2);
所以答案是:(0,2);
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:5,7,10,5,7,5,6,这组数据的众数和中位数分别是( )
A.10和7B.5和7C.5和6D.6和7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C,D为圆心,大于
 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( ) 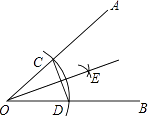
A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.O,E两点关于CD所在直线对称
D.C,D两点关于OE所在直线对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程mx﹣2=3x的解为x=﹣1,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠A=∠ADE,∠C=∠E.
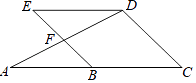
(1)若∠EDC=3∠C,求∠C的度数.
(2)求证:BE∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
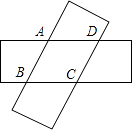
A.15
B.16
C.19
D.20
相关试题

