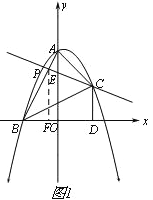
【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.

参考答案:
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)∵A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化得到△BCD,∴BD=OA=2,CD=OB=1,∠BDC=∠AOB=90°,∴C(1,1).
设经过A、B、C三点的抛物线解析式![]() ,则有
,则有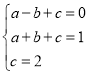 ,∴
,∴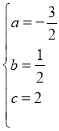 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图1所示,设直线PC与AB交于点E.∵直线PC将△ABC的面积分成1:3两部分,∴![]() 或
或![]() ,过E作EF⊥OB于点F,则EF∥OA,∴△BEF∽△BAO,∴
,过E作EF⊥OB于点F,则EF∥OA,∴△BEF∽△BAO,∴![]() ,∴当
,∴当![]() 时,
时,![]() ,∴EF=
,∴EF=![]() ,BF=
,BF=![]() ,∴E(
,∴E(![]() ,
,![]() ),∴直线PC解析式为
),∴直线PC解析式为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() (舍去),∴P(
(舍去),∴P(![]() ,
,![]() );
);
当![]() 时,同理可得,P(
时,同理可得,P(![]() ,
,![]() ).
).
(3)设△ABO平移的距离为t,△A1B1O1与△B2C1D1重叠部分的面积为S.
由平移得,A1B1的解析式为y=2x+2﹣t,A1B1与x轴交点坐标为(![]() ,0).
,0).
C1B2的解析式为![]() ,C1B2与y轴交点坐标为(0,
,C1B2与y轴交点坐标为(0,![]() ).
).
①如图2所示,当![]() 时,△A1B1O1与△B2C1D1重叠部分为四边形.
时,△A1B1O1与△B2C1D1重叠部分为四边形.
设A1B1与x轴交于点M,C1B2与y轴交于点N,A1B1与C1B2交于点Q,连结OQ.
由由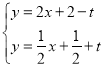 ,得
,得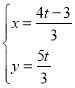 ,∴Q(
,∴Q(![]() ,
,![]() ),∴
),∴![]() =
=![]() ,∴S的最大值为
,∴S的最大值为![]() .
.
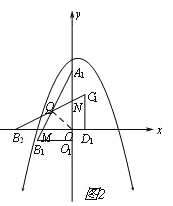
②如图3所示,当![]() 时,△A1B1O1与△B2C1D1重叠部分为直角三角形.
时,△A1B1O1与△B2C1D1重叠部分为直角三角形.
设A1B1与x轴交于点H,A1B1与C1D1交于点G,∴G(1﹣2t,4﹣5t),∴D1H=![]() ,D1G=4﹣5t,∴S=
,D1G=4﹣5t,∴S=![]() D1H×D1G=
D1H×D1G=![]() ,∴当
,∴当![]() 时,S的最大值为
时,S的最大值为![]() .
.
综上所述,在此运动过程中△ABO与△BCD重叠部分面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程mx﹣2=3x的解为x=﹣1,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
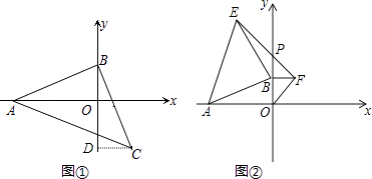
(1)如图①,等腰直角△ABC中,∠ABC=90°,AB=BC,点A、B分别在坐标轴上,若点C的横坐标为2,直接写出点B的坐标;(提示:过C作CD⊥y轴于点D,利用全等三角形求出OB即可)
(2)如图②,若点A的坐标为(﹣6,0),点B在y轴的正半轴上运动时,分别以OB、AB为边在第一、第二象限作等腰直角△OBF,等腰直角△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值.若变化,求PB的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠A=∠ADE,∠C=∠E.
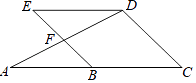
(1)若∠EDC=3∠C,求∠C的度数.
(2)求证:BE∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
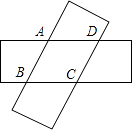
A.15
B.16
C.19
D.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,对角线AC=12.若过点A作AE⊥CD,垂足为E,则AE的长为( )
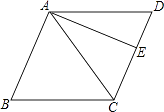
A.9
B.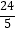
C.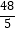
D.9.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
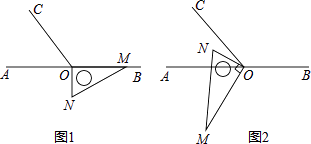
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
相关试题

