【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
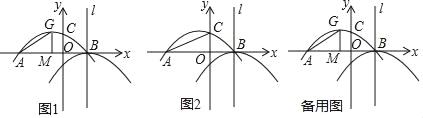
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)应用待定系数法求解析式;
(2)设出点T坐标,表示△TAC三边,进行分类讨论;
(3)设出点P坐标,表示Q、R坐标及PQ、QR,根据以P,Q,R为顶点的三角形与△AMG全等,分类讨论对应边相等的可能性即可.
(1)由已知,c=![]() ,
,
将B(1,0)代入,得:a﹣![]() =0,
=0,
解得a=﹣![]() ,
,
抛物线解析式为y1=![]() x2-
x2-![]() x+
x+![]() ,
,
∵抛物线y1平移后得到y2,且顶点为B(1,0),
∴y2=﹣![]() (x﹣1)2,
(x﹣1)2,
即y2=-![]() x2+
x2+![]() x-
x-![]() ;
;
(2)存在,
如图1:
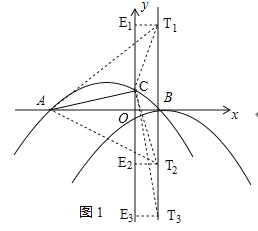
抛物线y2的对称轴l为x=1,设T(1,t),
已知A(﹣3,0),C(0,![]() ),
),
过点T作TE⊥y轴于E,则
TC2=TE2+CE2=12+(![]() )2=t2﹣
)2=t2﹣![]() t+
t+![]() ,
,
TA2=TB2+AB2=(1+3)2+t2=t2+16,
AC2=![]() ,
,
当TC=AC时,t2﹣![]() t+
t+![]() =
=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() ;
;
当TA=AC时,t2+16=![]() ,无解;
,无解;
当TA=TC时,t2﹣![]() t+
t+![]() =t2+16,
=t2+16,
解得t3=﹣![]() ;
;
当点T坐标分别为(1,![]() ),(1,
),(1,![]() ),(1,﹣
),(1,﹣![]() )时,△TAC为等腰三角形;
)时,△TAC为等腰三角形;
(3)如图2:
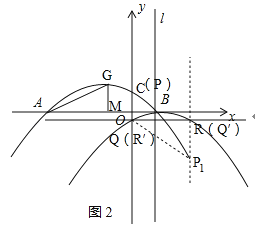
设P(m,![]() ),则Q(m,
),则Q(m,![]() ),
),
∵Q、R关于x=1对称
∴R(2﹣m,![]() ),
),
①当点P在直线l左侧时,
PQ=1﹣m,QR=2﹣2m,
∵△PQR与△AMG全等,
∴当PQ=GM且QR=AM时,m=0,
∴P(0,![]() ),即点P、C重合,
),即点P、C重合,
∴R(2,﹣![]() ),
),
由此求直线PR解析式为y=﹣![]() x+
x+![]() ,
,
当PQ=AM且QR=GM时,无解;
②当点P在直线l右侧时,
同理:PQ=m﹣1,QR=2m﹣2,
则P(2,﹣![]() ),R(0,﹣
),R(0,﹣![]() ),
),
PQ解析式为:y=﹣![]() ;
;
∴PR解析式为:y=﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有
 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台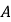 型和5台
型和5台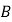 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台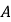 型和7台
型和7台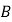 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台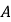 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台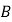 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.(1)分别求每台
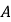 型,
型, 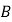 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?(2)若不同数量的
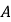 型和
型和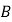 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元? -
科目: 来源: 题型:
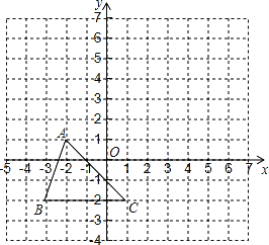
查看答案和解析>>【题目】 已知:如图,A(-2,1)B(-3,-2),C(1,-2)把△AEC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)画出△A'B'C';
(2)若点P(m,n)是△ABC边上的点,经上述平移后,点P的对应点为P',写出点P'的坐标为______;
(3)连接AA',CC',求出四边形A'ACC'的面积.
-
科目: 来源: 题型:
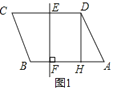
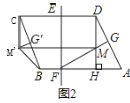
查看答案和解析>>【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
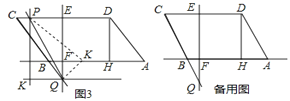
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图直线
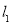 的解析式为y=x+1,直线
的解析式为y=x+1,直线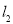 的解析式为
的解析式为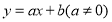 ;这两个图象交于y轴上一点C,直线
;这两个图象交于y轴上一点C,直线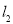 与x轴的交点B(2,0).
与x轴的交点B(2,0).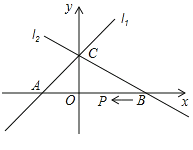
(1)求a、b的值;
(2)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
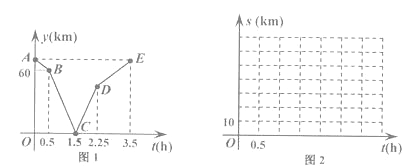
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
相关试题

