【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
参考答案:
【答案】(1)每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米;
型挖据机一小时挖土15立方米;
(2)共有三种调配方案.方案一: ![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;方案二:
型挖掘机5台;方案二: ![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;方案三:
型挖掘机4台;方案三: ![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.当A型挖掘机7台,
型挖掘机3台.当A型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.
【解析】(1)根据题意列出方程组即可;
(2)利用总费用不超过12960元求出方案数量,再利用一次函数增减性求出最低费用.
(1)设每台![]() 型,
型,![]() 型挖掘机一小时分别挖土
型挖掘机一小时分别挖土![]() 立方米和
立方米和![]() 立方米,根据题意,得
立方米,根据题意,得
![]()
解得![]()
所以,每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米.
型挖据机一小时挖土15立方米.
(2)设![]() 型挖掘机有
型挖掘机有![]() 台,总费用为
台,总费用为![]() 元,则
元,则![]() 型挖据机有
型挖据机有![]() 台.根据题意,得
台.根据题意,得
![]()
![]() ,
,
因为![]() ,解得
,解得![]() ,
,
又因为![]() ,解得
,解得![]() ,所以
,所以![]() .
.
所以,共有三种调配方案.
方案一:当![]() 时,
时,![]() ,即
,即![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;
型挖掘机5台;
方案二:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;
型挖掘机4台;
方案三:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.
型挖掘机3台.
![]() ,由一次函数的性质可知,
,由一次函数的性质可知,![]() 随
随![]() 的减小而减小,
的减小而减小,
当![]() 时,
时,![]() ,
,
此时![]() 型挖掘机7台,
型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.
-
科目: 来源: 题型:
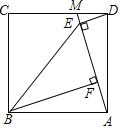
查看答案和解析>>【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.

(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2
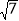 ,AC=2
,AC=2 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
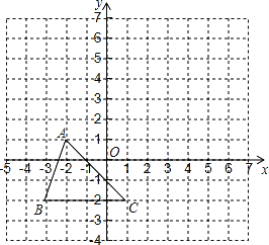
查看答案和解析>>【题目】 已知:如图,A(-2,1)B(-3,-2),C(1,-2)把△AEC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)画出△A'B'C';
(2)若点P(m,n)是△ABC边上的点,经上述平移后,点P的对应点为P',写出点P'的坐标为______;
(3)连接AA',CC',求出四边形A'ACC'的面积.
-
科目: 来源: 题型:
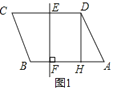
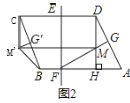
查看答案和解析>>【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
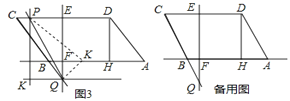
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y1=ax2﹣
 x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,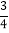 ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.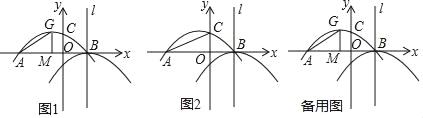
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
相关试题

