【题目】如图1,在![]() 中,
中,![]() 为锐角.点
为锐角.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
解答下列问题:
![]() 如果
如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 、
、![]() 之间的位置关系为________,数量关系为________.
之间的位置关系为________,数量关系为________.
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,为什么?
的延长线上时,如图3,①中的结论是否仍然成立,为什么?
![]() 如果
如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动.试探究:当
上运动.试探究:当![]() 满足一个什么条件时,
满足一个什么条件时,![]() (点
(点![]() 、
、![]() 重合除外)?画出相应图形,并说明理由.(画图不写作法)
重合除外)?画出相应图形,并说明理由.(画图不写作法)

参考答案:
【答案】(1)垂直,相等; ![]() 当
当![]() 时,
时,![]() ,理由见解析.
,理由见解析.
【解析】
(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;
(2)过点A作AG⊥AC交CB或CB的延长线于点G,于是得到∠GAC=90°,可推出∠ACB=∠AGC,证得AC=AG,根据(1)的结论于是得到结果.
(1)①正方形ADEF中,AD=AF.
∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF.在△DAB与△FAC中,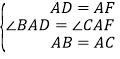 ,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.
,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.
故答案为:垂直、相等;
②成立,理由如下:
∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF
在△BAD与△CAF中,∵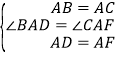 ,∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
,∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°,∴CF⊥BD;
(2)当∠ACB=45°时,CF⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°.
∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG.在△GAD与△CAF中,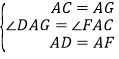 ,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为
 元时,每天能卖出
元时,每天能卖出 串,在此基础上,每加价
串,在此基础上,每加价 元李大妈每天就会少卖出
元李大妈每天就会少卖出 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一辆汽车油箱里剩油量
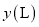 与行驶时间
与行驶时间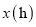 的图像,根据图像回答下列问题:
的图像,根据图像回答下列问题: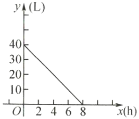
(1)汽车行驶前油箱里有______
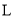 汽油;
汽油;(2)当汽车行驶
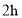 时,油箱里还有______
时,油箱里还有______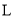 汽油;
汽油;(3)汽车最多能行驶______
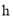 ,它每小时耗油______
,它每小时耗油______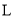 ;
;(4)油箱中剩油
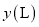 行驶时间
行驶时间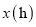 之间的函数关系式是______.
之间的函数关系式是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是一张边长为
是一张边长为 的正方形纸片,
的正方形纸片, ,
, 分别为
分别为 ,
, 的中点,沿过点
的中点,沿过点 的折痕将
的折痕将 角翻折,使得点
角翻折,使得点 落在
落在 上的点
上的点 处,折痕交
处,折痕交 于点
于点 ,求
,求 的长度.
的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一根弹簧的长度为10厘米,当弹簧受到
 千克的拉力时(
千克的拉力时( 不超过10),弹簧的长度是
不超过10),弹簧的长度是 (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:拉力
 (千克)
(千克)1
2
3
4
…
弹簧的长度
 (厘米)
(厘米)



…
(1)写出弹簧长度
 (厘米)关于拉力
(厘米)关于拉力 (千克)的函数解析式;
(千克)的函数解析式;(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:

时间t/h
0
0.2
0.3
0.4
路程s/km
(3)路程s可以看成时间t的函数吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校科技小组进行野外考察,途中遇到一片湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道,木板对地面的压强
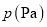 是木板面积
是木板面积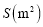 的反比例函数,其图像如下图所示:
的反比例函数,其图像如下图所示: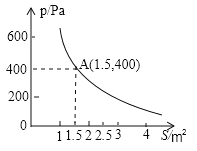
(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为
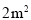 时,压强是多少?
时,压强是多少?(3)如果要求压强不超过
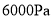 ,木板的面积至少要多大?
,木板的面积至少要多大?
相关试题

