【题目】如图,在△ABC中, AB的垂直平分线EF交BC于点E,交AB于点F, D为线段CE的中点, BE=AC.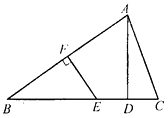
(1)求证: ![]()
(2)若 ![]() ,求∠B的度数.
,求∠B的度数.
参考答案:
【答案】
(1)解:连接AE,
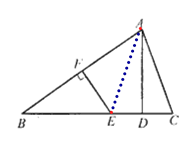
∵EF垂直平分AB,
∴AE=BE ,
∵BE=AC,
∴AE=AC,
∵D是EC的中点,
∴AD⊥BC.
(2)解:设∠B=x°,
∵AE=BE,
∴∠BAD=∠B=x,
∴∠AEC=2x,
∵AE=AC,
∴∠C=∠AEC=2x,
在三角形ABC中,3x+75°=180°.
x=35. ∴∠B=35°.
【解析】(1)根据垂直平分线的性质,线段垂直平分线上的点与线段的两个端点的距离相等;得到AE=AC,由D是EC的中点,根据等腰三角形的三线合一,得到AD⊥BC;(2)根据三角形内角和定理直接求出∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强
 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留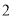 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚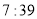 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早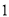 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程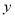 (千米)与行驶时间
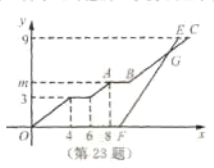
(千米)与行驶时间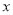 (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.(1)求点
 的纵坐标
的纵坐标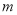 的值;
的值;(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项.现将调查结果绘制成如下所示的两幅统计图.

请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)若该校八年级共有
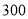 名学生,请你估计其中最喜欢排球的学生人数.
名学生,请你估计其中最喜欢排球的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+3)(x+n)=x2+mx﹣21,则m的值为( )
A.2B.﹣2C.4D.﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,抛物线
中,抛物线 交
交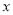 轴于
轴于 、
、 两点(点
两点(点 在点
在点 的左侧),将该抛物线位于
的左侧),将该抛物线位于 轴上方曲线记作
轴上方曲线记作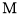 ,将该抛物线位于
,将该抛物线位于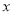 轴下方部分沿
轴下方部分沿 轴翻折,翻折后所得曲线记作
轴翻折,翻折后所得曲线记作 ,曲线
,曲线 交
交 轴于点
轴于点 ,连接
,连接 、
、 .
.(1)求曲线
 所在抛物线相应的函数表达式;
所在抛物线相应的函数表达式;(2)求
 外接圆的半径;
外接圆的半径;(3)点
 为曲线
为曲线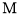 或曲线
或曲线 上的一个动点,点
上的一个动点,点 为
为 轴上的一个动点,若以点
轴上的一个动点,若以点 、
、 、
、 、
、 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)若2x+5y﹣3=0,求4x32y的值.
(2)若26=a2=4b , 求a+b值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y (厘米)与燃烧时间x (小时)之间的关系如图所示,其中乙蜡烛燃烧时y与x之间的函数关系式是
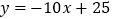 .
.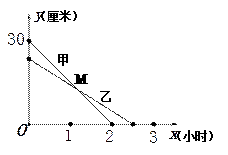
(1)甲蜡烛燃烧前的高度是厘米,乙蜡烛燃烧的时间是小时.
(2)求甲蜡烛燃烧时y与x之间的函数关系式.
(3)求出图中交点M的坐标,并说明点M的实际意义.
相关试题

