【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将该抛物线位于
的左侧),将该抛物线位于![]() 轴上方曲线记作
轴上方曲线记作![]() ,将该抛物线位于
,将该抛物线位于![]() 轴下方部分沿
轴下方部分沿![]() 轴翻折,翻折后所得曲线记作
轴翻折,翻折后所得曲线记作![]() ,曲线
,曲线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求曲线![]() 所在抛物线相应的函数表达式;
所在抛物线相应的函数表达式;
(2)求![]() 外接圆的半径;
外接圆的半径;
(3)点![]() 为曲线
为曲线![]() 或曲线
或曲线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,若以点
轴上的一个动点,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标.
的坐标.

参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)点
;(3)点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.
【解析】
试题分析:(1) 把![]() 化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线
化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线![]() 所在抛物线的顶点坐标和开口方向,即可得曲线
所在抛物线的顶点坐标和开口方向,即可得曲线![]() 的解析式;(2)先求得
的解析式;(2)先求得![]() 外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
试题解析:(1)因为![]() 可化为
可化为![]() ,
,
所以抛物线![]() 的点的坐标为(1,-4),开口向上,
的点的坐标为(1,-4),开口向上,
所以曲线![]() 所在抛物线的顶点坐标为(1,4),开口向下,
所在抛物线的顶点坐标为(1,4),开口向下,
故曲线![]() 所在抛物线相应的函数表达式为
所在抛物线相应的函数表达式为![]() ,
,
即![]() ;
;
(2)因为抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,
所以A(-1,0),B(3,0),则线段AB的垂直平分线的直线为x=1,
因为曲线![]() 交
交![]() 轴于点(0,3),
轴于点(0,3),
所以OC=OB,又∠COB=90°,所以线段BC的垂直平分线为直线y=x,
联立![]() ,解得
,解得![]() ,所以△ABC的外接圆圆心坐标为(1,1),
,所以△ABC的外接圆圆心坐标为(1,1),
由勾股定理可得![]() ,所以△ABC的外接圆半径为
,所以△ABC的外接圆半径为![]() ;
;
(3)过点C作直线l∥x轴,交曲线M或N于点P,
①当点P位于曲线M上时,
由![]() ,解得
,解得![]() ,
,
所以CP=![]() ,H或CP=
,H或CP=![]() ;
;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
②当点P位于曲线N上时,
由![]() ,解得
,解得![]() (舍去),
(舍去),
所以CP=2;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
综上所述,点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项.现将调查结果绘制成如下所示的两幅统计图.

请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)若该校八年级共有
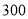 名学生,请你估计其中最喜欢排球的学生人数.
名学生,请你估计其中最喜欢排球的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+3)(x+n)=x2+mx﹣21,则m的值为( )
A.2B.﹣2C.4D.﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中, AB的垂直平分线EF交BC于点E,交AB于点F, D为线段CE的中点, BE=AC.
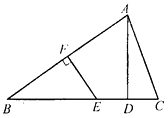
(1)求证:
(2)若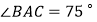 ,求∠B的度数.
,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)若2x+5y﹣3=0,求4x32y的值.
(2)若26=a2=4b , 求a+b值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y (厘米)与燃烧时间x (小时)之间的关系如图所示,其中乙蜡烛燃烧时y与x之间的函数关系式是
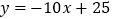 .
.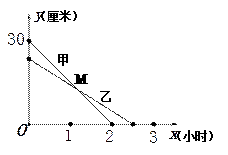
(1)甲蜡烛燃烧前的高度是厘米,乙蜡烛燃烧的时间是小时.
(2)求甲蜡烛燃烧时y与x之间的函数关系式.
(3)求出图中交点M的坐标,并说明点M的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边是 4,周长是 18,则它的腰长为____.
相关试题

