【题目】定义:点M,N把线段AB分割成AM、MN,NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)如图①,已知M、N是线段AB的勾股分割点,AM=6,MN=8,求NB的长;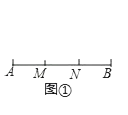
(2)如图②,在△ABC中,点D、E在边线段BC上,且BD=3,DE=5,EC=4,直线l∥BC,分别交AB、AD、AE、AC于点F、M、N、G.求证:点M,N是线段FG的勾股分割点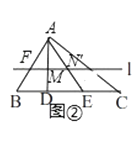
(3)在菱形ABCD中,∠ABC=β(β<90°),点E、F分别在BC、CD上,AE、AF分别交BD于点M、N.
①如图③,若BE= ![]() BC,DF=
BC,DF= ![]() CD,求证:M、N是线段BD的勾股分割点.
CD,求证:M、N是线段BD的勾股分割点.
②如图④,若∠EAF= ![]() ∠BAD,sinβ=
∠BAD,sinβ= ![]() ,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.
,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.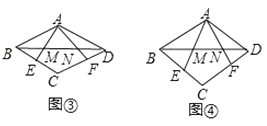
参考答案:
【答案】
(1)
解:当NB为最长线段时,
∵M、N是线段AB的勾股分割点,AM=6,MN=8,
∴NB= ![]() =10;
=10;
当MN为最长线段时,
NB= ![]() =2
=2 ![]() ,
,
综上所述,NB的值为10或2 ![]() ;
;
(2)
证明:如图2,∵BD=3,DE=5,EC=4,
∴DE2=BD2+EC2,
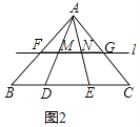
∵直线l∥BC,
∴![]() ,
,
∴可设![]() ,
,
∴FM=kBD,MN=kDE,NG=kEC,
∵DE2=BD2+EC2,
∴MN2=FM2+NG2,
∴点M,N是线段FG的勾股分割点;
(3)
解:①证明:如图3,∵四边形ABCD是菱形,
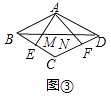
∴AD//BE,AB=BC=CD=DA,
∴△BEM∽△DAM,
∴![]() ,
,
∵BE=![]() BC,
BC,
∴BM=![]() DM,BM=
DM,BM=![]() BD,
BD,
同理可得,DN=![]() BD,
BD,
∴MN=BD﹣BM﹣DN=![]() BD,
BD,
∵MN2=![]() BD2,BM2+ND2=
BD2,BM2+ND2=![]() BD2+
BD2+![]() BD2=
BD2=![]() BD2,
BD2,
∴MN2=BM2+ND2,
∴M、N是线段BD的勾股分割点.
②如图4,将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,
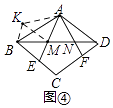
∴∠KBM=∠KBA+∠ABM=∠ABC,
∵sinβ=![]() ,
,
∴sin∠KBM=![]() ,
,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠KAM=∠NAM,
∵AN=AK,AM=AM,
∴△KAM≌△NAM,
∴KM=NM,
∵点M、N是线段BD的勾股分割点,
∴△KBM是直角三角形,
∵sin∠KBM=![]() ,
,
∴BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【解析】(1)分两种情况进行讨论:NB为最长线段;MN为最长线段,分别根据勾股定理进行计算即可;(2)根据BD=3,DE=5,EC=4,可得DE2=BD2+EC2 , 再根据直线l∥BC,可得 ![]() =
= ![]() ,故可设
,故可设 ![]() =
= ![]() =
= ![]() =k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出
=k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出 ![]() =
= ![]() ,再根据BE=
,再根据BE= ![]() BC,可得出BM=
BC,可得出BM= ![]() DM,BM=
DM,BM= ![]() BD,同理可得,DN=
BD,同理可得,DN= ![]() BD,进而得到MN=BD﹣BM﹣DN=
BD,进而得到MN=BD﹣BM﹣DN= ![]() BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM=
BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM= ![]() ,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【考点精析】通过灵活运用勾股定理的概念和图形的旋转,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论:①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.其中成立的个数是( )
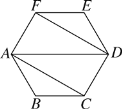
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AB=BC=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,点D的对应点为D′,连接D′B.若△D′BC为等边三角形,则DE=____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣  x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)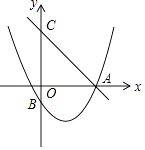
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】与图中的三角形相似的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.
(1)作△ABC的角平分线AD(尺规作图,保留痕迹);
(2)在AD的延长线上任取一点E,连接BE,CE.
①求证:△BDE≌△CDE;
②当AE=2AD时,四边形ABEC是平行四边形吗?请说明理由.
相关试题

