【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ![]() ,则a的值为 .
,则a的值为 .
参考答案:
【答案】-1
【解析】解:∵关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根, ∴ ![]() ,
,
解得:a<0,且a≠﹣2 ①
设抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点的坐标分别为(α,0)、(β,0),且α<β,
则α、β是关于x的方程x2﹣(2a+1)x+2a﹣5=0的两个不相等的实数根,
∵△=[﹣(2a+1)]2﹣4×1×(2a﹣5)=(2a﹣1)2+21>0,
∴a为任意实数②
由根与系数关系得:α+β=2a+1,αβ=2a﹣5.
∵抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别位于点(2,0)的两旁,
∴α<2,β>2,
∴(α﹣2)(β﹣2)<0,
∴αβ﹣2(α+β)+4<0,
∴2a﹣5﹣2(2a+1)+4<0
解得:a>﹣ ![]() ③
③
由①、②、③得a的取值范围是﹣ ![]() <a<0;
<a<0;
∵x1和x2是关于x的方程(a+2)x2﹣2ax+a=0的两个不相等的实数根
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∵﹣ ![]() <a<0,
<a<0,
∴a+2>0,
∴x1x2= ![]() <0.
<0.
不妨设x1>0,x2<0,
∴|x1|+|x2|=x1﹣x2=2 ![]() ,
,
∴x12﹣2x1x2+x22=8,即(x1+x2)2﹣4x1x2=8,
∴( ![]() )2﹣
)2﹣ ![]() =8,
=8,
解这个方程,得:a1=﹣4,a2=﹣1,
经检验,a1=﹣4,a2=﹣1都是方程( ![]() )2﹣
)2﹣ ![]() =8的根.
=8的根.
∵a=﹣4<﹣ ![]() ,舍去,
,舍去,
∴a=﹣1为所求.
所以答案是﹣1.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式组
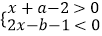 的解集为0<x<1,则a、b的值分别为( )
的解集为0<x<1,则a、b的值分别为( )
A.a=2,b=1
B.a=2,b=3
C.a=﹣2,b=3
D.a=﹣2,b=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为8cm,高AE长为
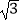 cm,则对角线AC长和BD长之比为( )
cm,则对角线AC长和BD长之比为( ) 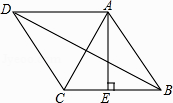
A.1:2
B.1:3
C.1:
D.1: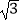
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=
 ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
相关试题

