【题目】已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC

(1)如图1,若∠AOC=30°,求∠DOE的度数。
(2)如图1,若∠AOC=![]() ,直接写出∠DOE的度数。(用含的代数式表示)
,直接写出∠DOE的度数。(用含的代数式表示)
(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出结论,并说明理由。
(4)在图2中,若∠AOC内部有一条射线OF,且满足∠AOC-4∠AOF=2∠BOE,其它条件不变,试写出∠AOF与∠DOE度数的关系(不写过程)
参考答案:
【答案】(1)15°;(2)∠DOE=![]()
![]() ;(3)证明见解析;(4)∠DOE=∠AOF+45°.
;(3)证明见解析;(4)∠DOE=∠AOF+45°.
【解析】
(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
(4)设∠DOE=x,∠AOF=y,根据已知和:∠AOC-4∠AOF=2∠BOE,结合图形可得出∠DOE=∠AOF+45°.
解:(1)∵∠AOC=30∴∠COB=150,
又 ∵OE平分∠BOC, ∴∠COE=75,
而∠COD=90,∴∠DOE=15 ;
(2)∠DOE=![]()
![]() ;
;
(3)设∠AOC=![]() ,则∠BOC=180-
,则∠BOC=180-![]() ,
,
又∵OE平分∠BOC, ∴∠COE=![]() (180°-
(180°-![]() =90°-
=90°-![]()
![]() .
.
又∵∠DOE=90,
∴∠DOE=90-(90-![]()
![]() )=-
)=-![]()
![]() ,
,
∴∠DOE=-![]() ∠AOC ;
∠AOC ;
(4)∠DOE=∠AOF+45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4
B.8
C.12
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AB=AC,点M、N在边BC上,且∠MAN=60°.若BM=2,CN=4,则MN的长为_____.
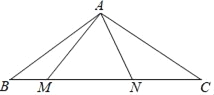
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
A.35°、145°
B.110°、70°
C.55°、125°
D.110° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-4-1-(-2)0+3÷
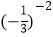 ;
;(2)(π-3)0+(
 )-2+4×2-1;
)-2+4×2-1;(3)(
 )-1+(π-2018)0-(-1)2019.
)-1+(π-2018)0-(-1)2019. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是________;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a18=________,an=________.
(2)欲求1+3+32+33+…+320的值,可令
S=1+3+32+33+…+320,①
将①两边同乘3,得__________________,②
由②减去①,得S=____________.
(3)用由特殊到一般的方法知:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,则an=________(用含a1,q,n的代数式表示).如果这个常数q≠1,求a1+a2+a3+…+an的值(用含a1,q,n的代数式表示).
相关试题

