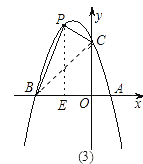
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
参考答案:
【答案】
(1)
解:将A(1,0),B(﹣3,0)代y=﹣x2+bx+c中得
![]()
∴ ![]() (3分)
(3分)
∴抛物线解析式为:y=﹣x2﹣2x+3
(2)
解:存在
理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称
∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小
∵y=﹣x2﹣2x+3
∴C的坐标为:(0,3)
直线BC解析式为:y=x+3
Q点坐标即为 ![]()
解得 ![]()
∴Q(﹣1,2)

(3)
解:存在.
理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0)
∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣ ![]()
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC
= ![]() BEPE+
BEPE+ ![]() OE(PE+OC)
OE(PE+OC)
= ![]() (x+3)(﹣x2﹣2x+3)+
(x+3)(﹣x2﹣2x+3)+ ![]() (﹣x)(﹣x2﹣2x+3+3)
(﹣x)(﹣x2﹣2x+3+3)
= ![]()
当x=﹣ ![]() 时,S四边形BPCO最大值=
时,S四边形BPCO最大值= ![]()
∴S△BPC最大= ![]()
当x=﹣ ![]() 时,﹣x2﹣2x+3=
时,﹣x2﹣2x+3= ![]()
∴点P坐标为(﹣ ![]() ,
, ![]() )
)
【解析】(1)根据题意可知,将点A、B代入函数解析式,列得方程组即可求得b、c的值,求得函数解析式;(2)根据题意可知,边AC的长是定值,要想△QAC的周长最小,即是AQ+CQ最小,所以此题的关键是确定点Q的位置,找到点A的对称点B,求得直线BC的解析式,求得与对称轴的交点即是所求;(3)存在,设得点P的坐标,将△BCP的面积表示成二次函数,根据二次函数最值的方法即可求得点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。

①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额
10
20
30
50
100
人数
2
4
5
3
1
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列大棚蔬菜种植情况统计图,回答问题:
(1)填上扇形统计图中括号中的数据;
(2)哪种蔬菜种植面积最大?
(3)哪两种蔬菜种植面积较接近?
(4)已知豆角种了27公顷,种植蔬菜的总面积是多少公顷?种植西红柿多少公顷?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:
 ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)图①中
 的值为 ;
的值为 ;(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为
 的约有多少只?
的约有多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )
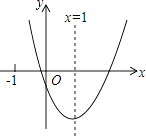
A.①②
B.①④
C.①③④
D.②③④ -
科目: 来源: 题型:
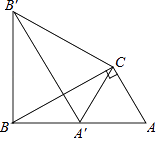
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
相关试题

