【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( ) 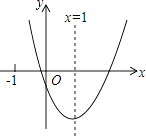
A.①②
B.①④
C.①③④
D.②③④
参考答案:
【答案】C
【解析】解:∵二次函数的图象的开口向上,
∴a>0,
∵二次函数的图象y轴的交点在y轴的负半轴上,
∴c<0,
∵二次函数图象的对称轴是直线x=1,
∴﹣ ![]() =1,
=1,
∴2a+b=0,b<0,
∴abc>0,∴①正确;
∵二次函数y=ax2+bx+c图象可知,当x>2时,y有小于0的情况,
∴②错误;
∵当x=﹣1时,y>0,
∴a﹣b+c>0,
把b=﹣2a代入得:3a+c>0,
∴③正确;
∵二次函数图象的对称轴是直线x=1,
∴﹣ ![]() =1,
=1,
∴2a+b=0,
∵a>0,
∴3a+b>0,故④正确.
故选C.
【考点精析】掌握二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点是解答本题的根本,需要知道二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列大棚蔬菜种植情况统计图,回答问题:
(1)填上扇形统计图中括号中的数据;
(2)哪种蔬菜种植面积最大?
(3)哪两种蔬菜种植面积较接近?
(4)已知豆角种了27公顷,种植蔬菜的总面积是多少公顷?种植西红柿多少公顷?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:
 ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(Ⅰ)图①中
 的值为 ;
的值为 ;(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为
 的约有多少只?
的约有多少只? -
科目: 来源: 题型:
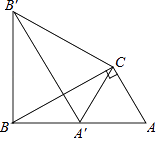
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C为⊙O上的一点,点D是
 的中点,过D作⊙O的切线交AC于E,DE=3,CE=1.
的中点,过D作⊙O的切线交AC于E,DE=3,CE=1. 
(1)求证:DE⊥AC;
(2)求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.

(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
相关试题

