【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE. 
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠A=∠AEB
(2)证明:∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
【解析】(1)根据圆内接四边形的性质得到∠A=∠DCE,根据等腰三角形的性质得到∠DCE=∠DEC,等量代换证明结论;(2)根据垂径定理得到OE是CD的垂直平分线,根据题意证明△DEC为等边三角形,证明结论.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆内接四边形的性质的理解,了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )
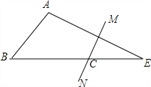
A. 45° B. 60° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车的速度为100千米/时,乙车的速度为80千米/时,___________小时后两车相距30千米.
【答案】
 或
或
【解析】
应该有两种情况,第一次应该还没相遇时相距30千米,第二次应该是相遇后交错离开相距30千米,根据路程=速度×时间,可列方程求解.
设第一次相距30千米时,经过了x小时,
由题意,得(100+80)x=450-30,
解得x=
 ;
;设第二次相距30千米时,经过了y小时,
由题意,得(100+80)y=450+30,
解得y=
 ,
,故经过
 小时或
小时或 小时相距30千米.
小时相距30千米.故答案为:
 或
或
【点睛】
本题考查理解题意能力,关键知道相距30千米时有两次以及知道路程=速度×时间,以路程做为等量关系可列方程求解.
【题型】填空题
【结束】
18【题目】如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是_________cm3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是_________cm3.

【答案】20
【解析】
利用正方形的性质以及图形中标注的长度得出AB=AE=5cm,进而得出长方体的长、宽、高进而得出答案.
如图:
 ,
,∵四边形ABCD是正方形,
∴AB=AE=5cm,
∴立方体的高为:(7-5)÷2=1(cm),
∴EF=5-1=4(cm),
∴原长方体的体积是:5×4×1=20(cm3).
故答案为:20.
【点睛】
此题主要考查了几何体的展开图,利用已知图形得出各边长是解题关键.
【题型】填空题
【结束】
19【题目】计算:
(1)-4-28-(-19)+(-24);
(2)-14÷(2017-π)0-(-
 )-2.
)-2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,BD是对角线.

(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
相关试题

