【题目】如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。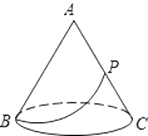
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果不取近似数)
参考答案:
【答案】
(1)解:∵主视图是边长为6m的正三形ABC,
∴AB母线AB=R=6m,
∴底面圆的半径r=3m,
∴S侧=![]() rR=
rR=![]() ×3×6=18
×3×6=18![]() (m2),
(m2),
(2)解:∵△ABC为正三角形,
∴BC=6,
∴l=2π×3=6π,
根据底面圆的周长等于展开后扇形的弧长,得: ![]() =6π,
=6π,
故n=180°,则∠BAC=90°,
∴BP= ![]() =3
=3 ![]() m
m
答:小猫所经过的最短路程是3 ![]() m.
m.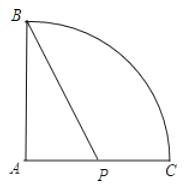
【解析】(1)由圆锥的侧面展开图是扇形,再根据圆锥的侧面积公式=![]()
![]() ×r×R计算即可.
×r×R计算即可.
(2)根据两点之间,线段最短;依题可得展开的是圆锥的半个侧面,再连接BP,再根据勾股定理计算即可.
【考点精析】利用弧长计算公式和扇形面积计算公式对题目进行判断即可得到答案,需要熟知若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个点到圆的最小距离为
 ,最大距离为
,最大距离为 ,则该圆的半径是____________.
,则该圆的半径是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4
 .
.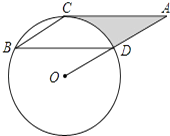
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个变量
 之间的变化情况如图所示,根据图像回答下列问题.
之间的变化情况如图所示,根据图像回答下列问题.(1)写出
 的变化范围;
的变化范围;(2)当
 时,求
时,求 的对应值;
的对应值;(3)当
 为何值时,
为何值时, 的值最大;
的值最大;(4)当
 在什么范围时,
在什么范围时, 的值在不断增加.
的值在不断增加.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )
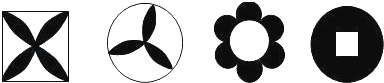
A.1个
B.2个
C.3个
D.4个
相关试题

