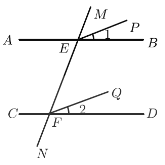
【题目】阅读理解填空,并在括号内填注理由.如图,已知AB//CD,M,N分别交AB,CD于点E,F,![]() ,求证:EP//FQ.
,求证:EP//FQ.
证明:![]() AB//CD(_________),
AB//CD(_________),
![]() (__________).
(__________).
又![]() (_____________)
(_____________)
∴![]() (___________)
(___________)
即:![]() ( )
( )
∴EP//______.(________).
参考答案:
【答案】见解析.
【解析】
根据两直线平行,同位角相等可得∠MEB=∠MFD,由两角的差根据等式的性质可得 ∠MEP=∠MFQ,再根据同位角相等,两直线平行即可证得结论.
∵AB//CD(已知),
∴∠MEB=∠MFD(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∠MEB-∠1=∠MFD-∠2(等式性质),
即:∠MEP=∠MFQ,
∴EP//FQ(同位角相等,两直线平行),
故答案为:已知;两直线平行,同位角相等;已知;等式性质;MFQ;FQ;同位角相等,两直线平行.
-
科目: 来源: 题型:
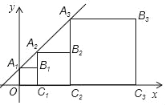
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A5的坐标是___.
-
科目: 来源: 题型:
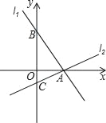
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线l1、l2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=
 .
.(1)求点B的坐标;
(2)若OC:OB=1:3,求直线l2的解析式.
-
科目: 来源: 题型:
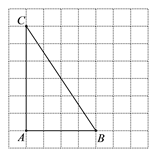
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P(不能借助圆规),使得
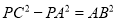 ,画出点P的位置,并说明理由.
,画出点P的位置,并说明理由.⑵ 求出⑴中线段PA的长度.
-
科目: 来源: 题型:
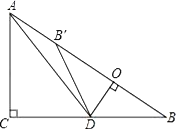
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).

(1)作出与△ABC关于x轴对称的△A1B1C1, 并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2, 使
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
相关试题

