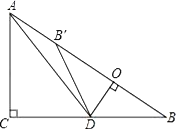
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
参考答案:
【答案】(1)证明见解析;(2)5;(3)![]()
【解析】试题分析:(1)公共角和直角两个角相等,所以相似.(2)由(1)可得三角形相似比,设BD=x,CD,BD,BO用x表示出来,所以可得BD长.(3)同(2)原理,BD=B′D=x,
AB′,B′O,BO用x表示,利用等腰三角形求BD长.
试题解析:
(1)证明:∵DO⊥AB,∴∠DOB=90°,
∴∠ACB=∠DOB=90°,
又∵∠B=∠B.∴△DOB∽△ACB.
(2)∵AD 平分∠CAB,DC⊥AC,DO⊥AB,
∴DO=DC,
在 Rt△ABC 中,AC=6,BC=,8,∴AB=10,
∵△DOB∽△ACB,
∴DO∶BO∶BD=AC∶BC∶AB=3∶4∶5,
设BD=x,则DO=DC=![]() x,BO=
x,BO=![]() x,
x,
∵CD+BD=8,∴ ![]() x+x=8,解得x=,5,即:BD=5.
x+x=8,解得x=,5,即:BD=5.
(3)∵点B 与点B′关于直线DO 对称,∴∠B=∠OB′D,
BO=B′O=![]() x,BD=B′D=x,
x,BD=B′D=x,
∵∠B 为锐角,∴∠OB′D 也为锐角,∴∠AB′D 为钝角,
∴当△AB′D 是等腰三角形时,AB′=DB′,
∵AB′+B′O+BO=10,
∴x+![]() x+
x+![]() x=10,解得x=
x=10,解得x=![]() ,即BD=
,即BD=![]() ,
,
∴当△AB′D 为等腰三角形时,BD=![]() .
.
-
科目: 来源: 题型:
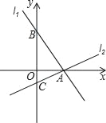
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线l1、l2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=
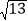 .
.(1)求点B的坐标;
(2)若OC:OB=1:3,求直线l2的解析式.
-
科目: 来源: 题型:
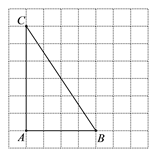
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P(不能借助圆规),使得
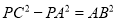 ,画出点P的位置,并说明理由.
,画出点P的位置,并说明理由.⑵ 求出⑴中线段PA的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解填空,并在括号内填注理由.如图,已知AB//CD,M,N分别交AB,CD于点E,F,
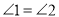 ,求证:EP//FQ.
,求证:EP//FQ.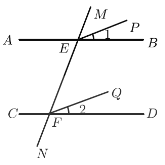
证明:
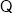 AB//CD(_________),
AB//CD(_________),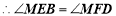 (__________).
(__________).又
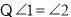 (_____________)
(_____________)∴
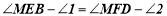 (___________)
(___________)即:
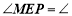 ( )
( )∴EP//______.(________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).

(1)作出与△ABC关于x轴对称的△A1B1C1, 并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2, 使
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
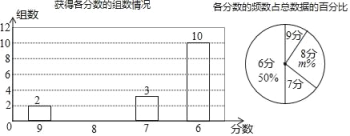
查看答案和解析>>【题目】目前由重庆市教育委员会,渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕,重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,重庆一中获优秀组织奖,重庆一中老师李珊获先进个人奖,其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛,若以下两个统计图统计了舞蹈组各代表队的得分情况:
(1)m= ,在扇形统计图中分数为7的圆心角度数为 度.
(2)补全条形统计图,各组得分的中位数是 分,众数是 分.
(3)若舞蹈组获得一等奖的队伍有2组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
相关试题

