【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况: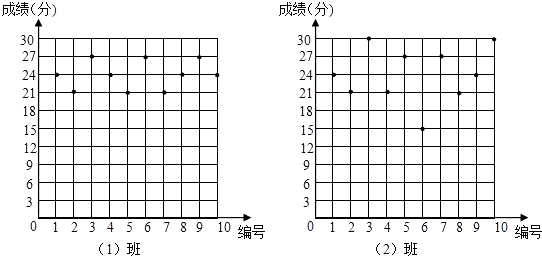
(1)利用图中提供的信息,补全下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | 24 | |
(2)班 | 24 |
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?
参考答案:
【答案】
(1)24,24,21
(2)解:(1)班成绩优秀人数=60× ![]() =42(名),(2)班成绩优秀人数=60×
=42(名),(2)班成绩优秀人数=60× ![]() =36(名)
=36(名)
答:(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀
(3)解:因为(1)班的极差=27﹣21=6,(2)班的极差=30﹣15=15,所以(1)班的学生纠错的整体情况更好一些
【解析】解:(1)
班级 | 平均数(分) | 中位数(分) | 众数(分) |
(1)班 | 24 | ||
(2)班 | 24 | 21 |
(2)(1)班成绩优秀人数=60× 7 10 =42(名),(2)班成绩优秀人数=60× 6 10 =36(名)
答:(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀
(3)因为(1)班的极差=27﹣21=6,(2)班的极差=30﹣15=15,所以(1)班的学生纠错的整体情况更好一些
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
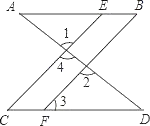
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
-
科目: 来源: 题型:
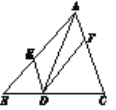
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.则下列说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中正确的是______(只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ A B C与
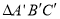 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:
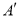 ______ ;
______ ; 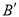 _______ ;
_______ ; 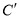 _______ ;
_______ ;(2)说明
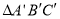 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.(3)若点
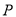 (
( ,
, 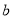 )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后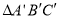 内的对应点
内的对应点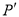 的坐标为 ________ ;
的坐标为 ________ ;(4)求△ A B C的面积..
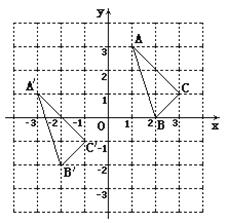
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
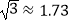 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
相关试题

