【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.

参考答案:
【答案】(1)证明见解析;(2)25.
【解析】分析:(1)由菱形的性质得出AB=CB,由等腰三角形的性质得出∠BAC=∠BCA,证出∠BAE=∠BCF,由SAS证明△BAE≌△BCF即可;(2)由菱形的性质得出AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
本题解析:
(1)证明:∵四边形ABCD是菱形,
∴AB=CB,
∴∠BAC=∠BCA,
∴180°﹣∠BAC=180°﹣∠BCA,
即∠BAE=∠BCF,
在△BAE和△BCF中, 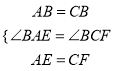 ,
,
∴△BAE≌△BCF(SAS);
(2)解:若∠ABC=40°,则当∠EBA=25°时,四边形BFDE是正方形.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,
∠ABC=20°,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
又∵AC⊥BD,∴四边形BFDE是菱形,
∵∠EBA=25°,
∴∠OBE=25°+20°=45°,
∴△OBE是等腰直角三角形,
∴OB=OE,
∴BD=EF,
∴四边形BFDE是矩形,
∴四边形BFDE是正方形;
故答案为:25.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A.π
B.
C.3+π
D.8﹣π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣
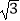 x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣  (x﹣
(x﹣ 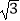 )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
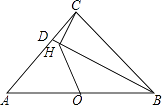
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元.购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)实验中学实际需要一次性购买足球和篮球共96个.要求购买足球和篮球的总费用不超过5800元,这所中学最多可以购买多少个篮球?
相关试题

